Tubular stand

There were a number of partial solutions but this well explained one is almost entirely the work ofAndrei of Tudor Vianu National College and shows how "obvious" the answer is with a little visualising and careful reasoning.

Image

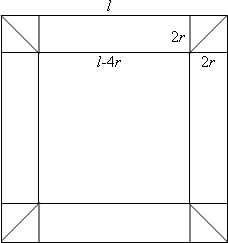
Let $l$ be the exterior length of the cylinders and $r$ - the radius of the cylinders.

In the first solution, I have $4$ cylinders (the $4$ squares length $l-4r$ and $2r$) and $8$ half-cylinders - cylinders cut through the diagonal (the 8 small right-angled triangles from the figure).

Each of the four cylinders has the volume: $ V_1 = \pi r^2 (l - 4r)$

Each of the half-cylinders has a volume of half a cylinder: $ V_2 = \frac{1}{2} \times \pi r^2 \times 2r = \pi r^3$ Now, the total volume of the tubular stand is: $ V = 4 \times V_1 + 8 \times V_2 = 4\pi r^2 (l - 2r) $

With the second method, I arrange the $8$ half-cylinders to make $4$ bigger cylinders, and these $4$ to the bigger ones. The height of one 'big' cylinder is $(l - 2r)$, and the total volume is: $$ V = 4 \pi r^2 (l - 2r) $$ which is exactly the result obtained above. Substituting the numerical values: $l = 10 \; \text{cm}$ and $r =0.5 \; \text{cm}$, I obtain:

$$ V = 4 \pi \times 0.25 \times(10 - 1) = 9 \pi = 28.27 \; {\text{cm}}^3 $$

If the volume wood would be double $(18 \pi)$, then the outside dimension of the dowel would be: \begin{eqnarray} 18 \pi &=& 4\pi \times 0.25 (l -1) \\ l - 1 & =& 18 \; \text{cm}\\ l &=& 19 \; \text{cm}\end{eqnarray} If the volume of wood would be the same but the radius would be $1 \; \text{cm}$, then the outside dimension would be: \begin{eqnarray} 9 \pi &=& 4\pi (l - 2) \\ l - 2 &=& \frac {9}{4} \\ l &=& 4.25 \; \text{cm}\end{eqnarray} The general formula for the volume of the dowel (proved above) is: $$ V = 4 \pi r^2 (l - 2r) $$ One could see that the volume is proportional to the square of the radius, and in the limit of long outside dimensions, proportional to the outside dimension.