Sliced
An irregular tetrahedron has two opposite sides the same length a
and the line joining their midpoints is perpendicular to these two
edges and is of length b. What is the volume of the tetrahedron?
Problem
Image
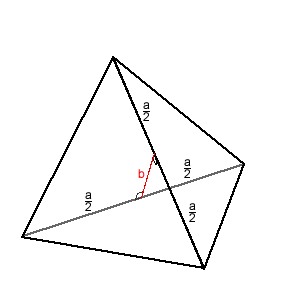
An irregular tetrahedron has two opposite sides the same length ($a$ say) and the line joining their midpoints is perpendicular to these two edges and is of length $b$. What is the volume of the tetrahedron?
Getting Started
Image
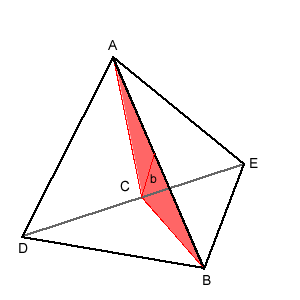
Slice the tetrahedron in two with a cut through the line $b$ and one of the equal edges. The perpendiculars are very important because of what you need to find the volume of a pyramid. You now have two identical pyramids like this:
Image
Student Solutions
Daniel, from Wales High School, sent us this very elegant solution:
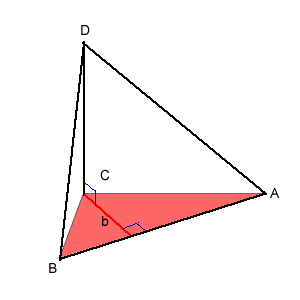
The formula for the volume of a tetrahedron is $$1/3 \times \text{area of base} \times \text{perpendicular height}$$ If you slice the tetrahedron in half through $b$ you end up with two equal smaller pyramids. I will work out the volume of one and then multiply by $2$ because they have equal volumes. So to start, I must work out the area of the base. The area of a triangle is calculated as follows: $$1/2 \times \text{base} \times \text{perpendicular height}$$ The base is $a$ and the perpendicular height is $b$ so the area of the base is $$(1/2)\times a\times b=(a b/2)$$ So using the formula for the volume of a pyramid: $$\text{Volume}=(1/3) \times (ab/2)\times (a/2)=a^2b/12$$ Times this by $2$ to get the volume for the big tetrahedron: $$(a^2b/12)\times 2=2a^2b/12 =a^2b/6$$ So the volume of the big tetrahedron is $a^2b/6$.
Teachers' Resources
This is quite a difficult problem to visualise.
A model of the solid made from the two "halves" may help pupls to see the symmetry.
