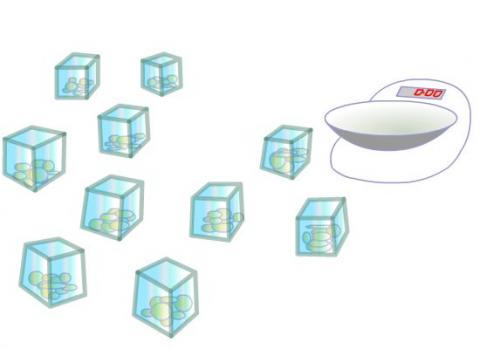
Money Measure
How can you use just one weighing to find out which box contains
the lighter ten coins out of the ten boxes?
Problem
You have ten identical open-topped boxes with 10 visually identical coins in each.
In nine of the boxes each of the 10 coins has a mass of 10g.
In one box the 10 coins have masses of only 9g each.
How can you find which box is the odd one out?
You have a normal mass measurer with a single pan and a scale. With just one weighing you can identify the box with the lighter coins.
What will you weigh?
Getting Started
How can you make one weighing that will tell you something about all the boxes at once?
How many boxes are different?
Is it worth taking different coins out of the different boxes?
Student Solutions
Excellent solutions were received from several of you including Heather from Stow Heath Junior School, Konrad from Baulkham Hills High and Richard from Sullivan School. Heather explains how you might go about finding the odd box:
Take one coin from the first box, two coins from the second box and so on. You will end up with 55 coins taken from the various boxes. Weigh the 55 coins. If the weight reads one gram less than 550 then 1 coin weighs 9 grams and box number 1 contains the light coins. If the weight reads 2 grams less than 550 then two coins weigh 9 grams and box number two contains the light coins and so on.
Konrad puts it a slightly different way:
The last digit of the weight will tell you which box has the 9g coins in it. If the last digit is 9 then the box you took 1 coin out of is the box you are looking for. If the last digit is 8 then the box you took 2 coins out of is the box you are looking for. If the last digit is 7 then the box you took 3 coins out of is the box you are looking for and so on.
Thank you to everyone for your solutions and sorry that we can't mention you all.
Teachers' Resources
Why do this problem?
This problem involves thinking 'out of the box'. The pupils need to work out a way of making one weighing of all the boxes that will give them information about all the different boxes at once.