On the Edge
If you move the tiles around, can you make squares with different coloured edges?
Problem
Here are four tiles:
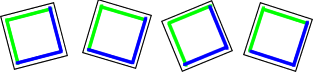
They can be arranged in a $2$ by $2$ square so that this large square has a green edge:

If the tiles are moved around, we can make a $2$ by $2$ square with a blue edge:

If I had nine tiles it would be quite easy to paint them so that, when they were arranged in a $3$ by $3$ square, the edge of this large square is green. I would need four tiles for the corners of the square, four tiles for the edges and one tile would go in the middle of the square so wouldn't need painting at all.
This is how the green-edged square would be made:

But I also want to be able to make a square with a blue edge and another square with a yellow edge.
How can the other sides of these tiles be painted so that all nine tiles can be rearranged to make two more $3$ by $3$ squares - one with a blue edge and one with a yellow edge?
Now try to colour sixteen tiles so that four $4$ by $4$ squares can be made - one with a green edge, one with a blue edge, one with a yellow edge and one with a red edge.
Find a way to colour $25$ tiles so that five $5$ by $5$ squares can be made, each with a differently coloured edge.
Do you think this is possible for $36$ tiles and six coloured edges?
Will it always be possible to add an extra colour as the squares get larger?
For a 3D version of this problem why not try " Inside Out "?
Click here for a poster of this problem.
Getting Started
Take one colour at a time and see how many edges are being used up on the edge of the big square.
Once the edges have been used they can be 'hidden' in the middle
Student Solutions
Adam of Moorside School sent us in his description of a possible painting for the three by three square:
The outside of the square should be green. The rest of one of the corner squares should be yellow. The rest of another corner square should be blue. The other two corner squares should have one side blue and the other side yellow. Then two of the squares in between the corner squares should have two touching sides yellow and one side blue. The other two squares in between the corner squares should have two touching sides blue and one side yellow. The middle square should be half yellow, half blue.
Adam's square looks like this:



Jenny made a prediction:
``I noticed that in an $n \times n$ square there are a total on $n^2$ small squares, and therefore a total of $4 n^2$ edges to be coloured. Each colour takes up $4 n$ of these edges, so it should be possible to colour an $n \times n$ square with $n$ different colours. To do this, we need to arrange for all the colours to have four cornerpieces and $4 (n-2)$ edge pieces."
Teachers' Resources
Why do this problem?
This problem is a familar context involving perimeters and squares that requires careful analysis. There are opportunities to experiment but a need to think ahead.
Possible approach
Arrange nine large squares into a $3 \times 3$ array and colour the edges - counting from $1$ to $12$ this time.
Rearrange the nine squares in a haphazard way to enable you to colour the edges in a different colour (counting $1$ to $12$).
"Does this mean we cannot do it?"
or
When any pair is successful challenge them to repeat the task:
"Well done. Would you be able to do this again without making any "false moves"?"
"Can we use more colours when we have $16$ squares?"
"How about with $25$ squares...?"
Key questions
Can you anticipate where certain squares will have to go in future rounds?
Possible support
Lots of paper squares so students do not have to worry about making mistakes.
A $4 \times 4$ array is probably easier.
Possible extension
Can students do all three colourings without rearranging the squares?
Will it always be possible to add an extra colour as the squares get larger?
For a 3D version of this problem students could try Inside Out
