Thousand Words
Here the diagram says it all. Can you find the diagram?
Problem
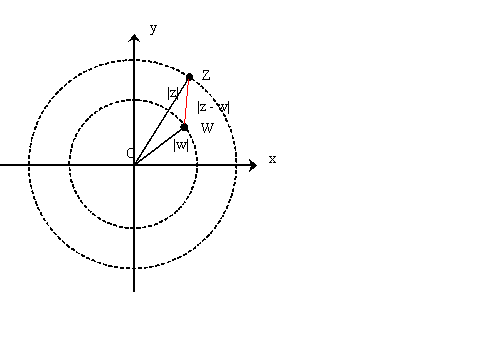
Draw a simple diagram which makes it clear that the following inequality holds for any complex numbers $z$ and $w$
$$|z-w|\geq |z| -|w|$$
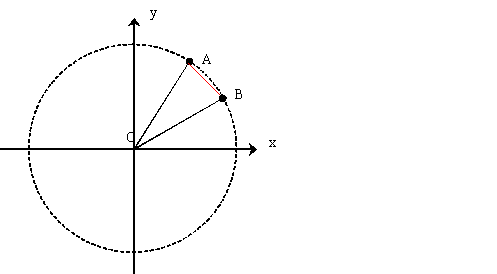
Now draw another simple diagram which makes it clear that the following inequality holds for any real numbers $\alpha> \beta$
$$|e^{i\alpha}-e^{i\beta}|\leq \alpha - \beta$$
Getting Started
Student Solutions
Thank you to Roy M. from Allerton High School and Andrei L. from Tudor Vianu National College, Bucharest, Romania for their solutions.
Draw two concentric circles with centres at the origin and radii $|z|$ and $|w|$ and suppose, without loss of generality, that $|z|> |w|$ then $z$ lies somewhere on the outer circle and $w$ lies somewhere on the inner circle.
Teachers' Resources
Why do this problem?
This problem encourages students to think about complex numbers geometrically in order to prove certain general results. It links work on modulus-argument form and exponential form of complex numbers with ideas from vectors, triangles and circles.
Possible approach
Students may work on this short problem individually or in pairs. They can be prompted to think about how they might represent $z$, $w$ and $z-w$ and how they might generalise the positions of $z$ and $w$ for any argument but a fixed modulus.
Once students have arrived at a suitable diagram to demonstrate the first result, they should be able to draw a suitable diagram to represent the second situation independently. They may be prompted to consider the modulus of $e^{i\alpha}$ and $e^{i\beta}$. Having drawn a suitable diagram, they will need to explain clearly what their diagram shows.
In both cases, care will need to be taken over arguments greater than $2\pi$.
Key questions
How can you represent $z$, $w$ and $z-w$ in an Argand diagram?
What does the modulus of each complex number represent geometrically? For fixed $|w|$ and $|z|$, what are the maximum and minimum values for $|z-w|$ and in what situations do they occur?
How can we generalise the diagram for fixed $|w|$ and $|z|$ but any argument?
How are $e^{i\alpha}$ and $e^{i\beta}$ the same as $|w|$ and $|z|$ and how are they different?
Possible extension
Students could be encouraged to write down another inequality for the maximum value of $|z-w|$ and also to explain carefully when (if) equality occurs for each of their relationships.
Possible support
Students could be prompted to draw the locus of $|z|=a$ for a fixed $a$ and the locus of $|w|=b$ for a fixed $b$ such that $${a}>{b}$$, as a starting point and asked to consider possible examples of $z-w$.
