Climbing
Sketch the graphs of y = sin x and y = tan x and some straight
lines. Prove some inequalities.
Problem
By considering the graph of $y=\sin x$ prove that, for $0\leq x \leq \pi/2$, $${2x\over \pi} \leq \sin x \leq x.$$ By considering the graph of $y=\tan x$ prove that, for $0 < a < b < \pi/2$, $${\tan a \over \tan b} < {a\over b}.$$
Can you find similar inequalities which hold for different ranges of $x$?
Getting Started
For the first part draw the graph of $\sin x$, draw the line segment joining the origin to the point $(\pi/2, 1)$ and draw the line $y=x$.
For the second part draw the graph of $\tan x$ and draw straight line segments joining the origin to the points $(a, \tan a)$ and $(b, \tan b)$.
Student Solutions
Thank you Andrei Lazanu from Tudor Vianu National College, Bucharest, Romania for this solution.
To solve the problem, I plotted three functions for $0 \leq x \leq \pi/2$. Below are the graphs of the three functions, all three plotted on the same figure with $y_1={2x\over \pi}$ in blue, $y_2 = \sin x$ in green and $y_3=x$ in red.
Image
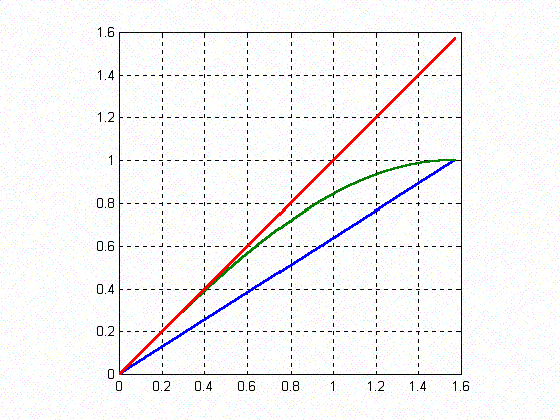
As seen from the figure, the green graph (i.e. $y = \sin x$) is situated between the other two graphs in the range of $0 \leq x \leq \pi/2$. For all $x$ between 0 and $\pi/2$ the point $(x, \sin x)$ is above the point $(x, 2x/\pi)$ and hence $${2x\over \pi} \leq \sin x.$$ In this interval the graph of $\sin x$ lies below the line $y=x$ because this line meets the graph of $\sin x$ at the origin and the gradient of $\sin x$ is less than 1 for all $x$. Hence $\sin x \leq x$.
For the second part of the problem, I have to prove that: $${\tan a \over \tan b} < {a \over b}.$$ For any $a$ and $b$ in this interval, both $a$, $b$, $\tan a$ and $\tan b$ are positive, so that the original inequality is equivalent to the following one: $${\tan a \over a} < {\tan b \over b}$$ In the figure below the graph of function $y=\tan x/x$ is plotted for $0 < x < \pi/2$.
Image
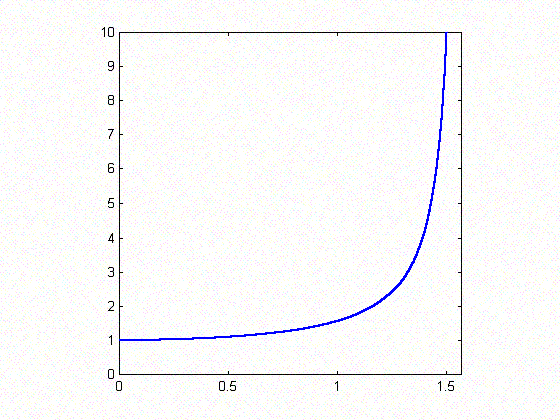
I observe that the function is monotonically increasing. This means that for any $a < b$ (but remaining in the interval $0 < a < b < \pi/2$), $y(a) < y(b)$ as required.
Alternatively, from the graph of $y = \tan x$ in this interval, if $a < b$ then the gradient of line joining the origin the point $(a, \tan a)$ is less than the gradient of the line joining the origin to the point $(b, \tan b)$ so $${\tan a \over a} < {\tan b \over b}$$ and hence $${\tan a \over \tan b} < {a \over b}.$$
Teachers' Resources
The graph of $y=\sin x$ lies above the line $y=2x/\pi$ joining the
origin to the point $(\pi/2, 1)$. The graph of $\sin x$ lies below
the line $y=x$. Why? What does this tell you about $\sin x$?
