Lots of Lollies
Frances and Rishi were given a bag of lollies. They shared them out evenly and had one left over. How many lollies could there have been in the bag?
Problem

Frances and Rishi were given a bag of lollies.
They shared them out equally and had one left over.
Just as they had finished sharing them their friends Kishan, Hayley and Paul came along. They wanted some lollies too so the children shared them out again between all of them. This time they had two lollies left over.
How many lollies could there have been in the bag?
Once you've had a chance to think about it, click below to see how three different groups of pupils began working on the task.
Sarah, Danielle and Sally said:
"We noticed that $17$ works as when there are only two of them they get $8$ each, with one left over. But when their friends come along they get three each with $2$ left over.
We also notice that $7$ works and $27$ works, as well as $107$."
Poppy began like this:
If the two children end up with one lolly it must be an odd number of lollies. Then three more children come making the total number of children $5$. Say they had $1$ lolly each when they shared them, the number of lollies would be $7$ because $1$ times $5$ is $5$ add on $2$ for the left over ones and it makes seven. If we carry this on to $10$ lollies each it shows:
$1$ lolly each - $7$ lollies
$2$ lollies each - $12$ lollies
$3$ lollies each - $17$ lollies
$4$ lollies each - $22$ lollies
$5$ lollies each - $27$ lollies
$6$ lollies each - $32$ lollies
$7$ lollies each - $37$ lollies
$8$ lollies each - $42$ lollies
$9$ lollies each - $47$ lollies
$10$ lollies each - $52$ lollies
Here is the start of Phoebe and Alice's work:
Can you take each of these starting ideas and develop it into a solution?
Can you adapt each of these strategies to find the number of lollies when there are three friends to start with and two friends join them?
How many lollies could there be in the bag if there was 1 lolly left over to start with, and then 1, 2, 3 or 4 lollies left when they were shared between the five children?
Or 2 lollies left over to start with...?
What if we started with four friends, and two more friends join them...?
Getting Started
How many children are there altogether when they share the lollies the second time?
Try using counters or blocks instead of lollies to help.
What is the smallest number of lollies there could be?
Is this the only number of lollies there could be?
Student Solutions
Thank you to everybody who sent in their ideas about this activity.
Dean started with the idea that there might be 17 lollies, and thought about what would happen if there were four friends to start with, and two more friends joined them:
There are 17 lollies because the two of them both got eight and when the friends came there were five so they all got three and 2 were left over because 15 were handed out.
If you start with 4 friends each will get 4 with one left over. If two more friends come they all get 2 with 5 left over.
Pooja at the International School in the Seychelles sent this message:
To get my answer I used the two times table. When there were two kids my answer was three. Then I used the five times table when three more kids came along. I said that if each child gets one and two leftover it must mean that the answer must be seven.
Felix from Henleaze Junior wrote:
First I worked out that there were two children and one lolly left over. So I tried 3. But then I worked out that there were then three more children which made 5 so it couldn't be 3. Then I worked out that there were two remaining when 3 more people came and I added the total number of people to the two remaining lollies and got 7. Then I went back to the two people and checked if it would work with the two people and it did, so one possible answer is 7.
But after that I figured out that if you add 10 it would mean that there were 17 lollies and it will still work because 2 people would then have 8 each and one remaining and 5 people would have 3 each and two remaining.
Adelle and Amanie, also at the International School in the Seychelles wrote:
With two people it must be odd.
With five people, we know 7 works.
We tried adding 5 but it came to an even number. Then we added 10, it always works.
These numbers work with 2 people: 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61
These numbers work with 5 people and 2 people: 7, 17, 27, 37, 47, 57, 67, 77, 87, 97, 107, 117, 127, 137, 147, 157, 167, 177, 187, 197, 207, 217

Children from Culgaith School in the UK sent in the following:
Nathan said that the answer has to be an odd number as it is shared between two children with 1 left over. We found the first solution was 7 - Emma said this. We then tried to find out if there were any other answers. We tried 8 - but then realised that this was an even number so we looked at 9 - too many left over. We looked at 11 - this time too few left over.
Alex suggested 17 - why did he choose this? He said the numbers were "basically the same". Mr Dodd said this wasn't quite true as he would rather have 17 chocolate bars than 7!
Millie said that the 10 lollipops different between 7 and 17 would give each of the two children two lollipops each and so 17 would work. We checked this out and it did! We then used the number square to show us all the solutions up to 100 - they all end in "7". We worked out that this was because the tens digit would always share out evenly between 5 children and the 7 would give each child 1 lollipop and have two left over.
Poppy from Steeple Morden Primary wrote:
If the two children end up with one lolly it must be an odd number of lollies. Then 3 more children come making the total number of children 5. Say they had 1 lolly each when they shared them, the number of lollies would be seven because 1 times 5 is 5 add on 2 for the left over ones and it makes seven.
If we carry this on to 10 lollies each it shows:
1 lolly each- 7 lollies
2 lollies each- 12 lollies
3 lollies each- 17 lollies
4 lollies each- 22 lollies
5 lollies each- 27 lollies
6 lollies each- 32 lollies
7 lollies each- 37 lollies
8 lollies each- 42 lollies
9 lollies each- 47 lollies
10 lollies each- 52 lollies
You can see here that it goes up in 5s each time. The answers that are possible are the ones where the children have an odd number of lollies.
It is most probable that they will have less than 27 lollies in their bag but this is not certain they could have 5007 lollies in the bag and 1001 each leaving two left over!
Thank you Poppy. I like the way you have thought about the practical side of the problem at the end and have decided how many lollies the children are likely to have had.
Stella from Chigwell School in England wrote a very thorough account of the challenge:
Any number ending in 7 works as if you divide it by 2 you get 1 left over and if you divide it by 5 you get 2 left over which fits in with the problem.
Because they start off with 2 children and they share them out equally you have to divide by 2 but so that it doesn't go in exactly you have 1 left over which means that it has to be an odd number. But when they have just finished sharing them out properly 3 more children come along making the total of children go up to 5, so now you have to divide by 5 so it can't be anything ending in 9, 3, 5 or 1 so that only leaves 7.
Simran from Maurice Hawk School in the USA, also had a very systematic approach. He said:
At first, I noticed that the number of lollies that I was splitting had to be an odd number or there would not have been anything left over. So, I made this table:

The blue shows the number of lollies that Francis and Rishi share and the purple shows the lollies that Frances, Rishi, Kishan, Hayley and Paul share. I tried a few different odd numbers and found that only a total of 7 lollies worked. Then I saw that 17 also works. Then I thought of the 100s chart and the 7s column. All the numbers in that column would work. I checked with a big number like 87 and it worked.
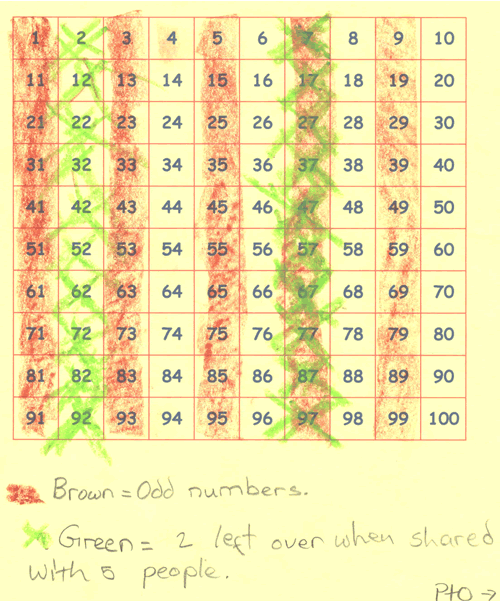
I think Simran's solution links very closely with this next one... Phoebe and Alice from Cambridge used a 100 square to help solve the problem. Here is Alice's square:

And here is Phoebe's:

You can see that they have shaded all the odd numbers in brown and put a green cross through all the numbers that have 2 left over when shared between 5. They conclude that the number of lollies in the bag could be:
... any number that ends with a 7: 7, 17, 27, 37, 47, 57, 67, 77, 87, 97 ...
Well done both of you - you have shown how the number square is a very useful tool.
Several pupils from Warren Road Primary School sent solutions, including Ayush, Vihaan, Vishwaksen and Sarthak. This solution summarised their findings:
The two conditions:
When there are two children, 1 lollipop must be left over.
When there are five children, 2 lollipops must be left over.
At the beginning, there are two children. They share the lollies evenly. If the bag has 7 lollies, they could give themselves 3 each and there would be 1 left over. But then their friends come along. Now there are 5 people. Still with 7 lollies, they could give themselves 1 each and have 2 leftover. This meets the requirements, so 7 is one of the answers.
After working out this solution, we realised the pattern:
When the number 5 is multiplied by any odd number and has 2 added to it, it is a solution of how many lollies are in the bag.
You have expressed this in a general way, which is very helpful. Mathematicians love to generalise!
Thank you for all these solutions which were all thought about in a slightly different way. There usually are a variety of possible ways of approaching problems.
Teachers' Resources
Why do this problem?
In conjunction with the other tasks in this group, this task also offers the chance to focus on any of the five key ingredients that characterise successful mathematicians.
Possible approach
You could introduce this challenge by acting it out. Invite two children to the front of the class and ask everyone to imagine that you have a bag of lollies. Explain that you give them out to the two volunteers so that they have the same number each, but there is one left in the bag. You could mime giving out some lollies so that everyone gets the idea. Then invite three more children to the front. Mime gathering the lollies back into the bag and then distributing them equally again, this time explaining that you have two left over. Pose the question "I wonder how many lollies could have been in the bag?".
Give the class a few minutes to consider, individually, how they might go about tackling the problem, then pair them up and suggest that they talk to their partner about their ideas so far. Try to stand back and observe, and resist the temptation to make helpful suggestions!
Allow pairs to work on the task so that you feel they have made some progress, but do not worry if they have not completed it or if they report being stuck. The aim at this stage is for everyone to 'get into' the problem and work hard on trying to solve it, but not necessarily to achieve a final solution.
At a suitable time, hand out this (doc, pdf) to pairs. Suggest to the class that when they've finished or can't make any further progress, they should look at the sheet showing three approaches used by children working on this task. Pose the question, "What might each do next? Can you take each of their starting ideas and develop them into a solution?". You may like pairs to record their work on large sheets of paper, which might be more easily shared with the rest of the class in the plenary.
Allow at least fifteen minutes for a final discussion. Invite some pairs to explain how the three different methods might be continued. You may find that some members of the class used completely different approaches when they worked on the task to begin with, so ask them to share their methods too. You can then facilitate a discussion about the advantages and disadvantages of each. Which way would they choose to use if they were presented with a similar task in the future? Why?
Key questions
How many children are there altogether when they share the lollies the second time?
What is the smallest number of lollies there could be?
Is this the only number of lollies there could be?
Tell me about this approach. What do you think she/they were doing?
How do you think this will help to solve the problem?
What do you think she/they would have done next?
Possible extension
How many lollies could there be in the bag if there was 1 lolly left over to start with, and then 1, 2, 3 or 4 lollies left when they were shared between the five children?
Or 2 lollies left over to start with...?
Possible support
Learners might request a range of different resources to help them tackle this challenge, for example a hundred square, or some counters/cubes. Try not to pre-empt their requests by placing equipment out on tables at the start, but do make sure these kind of resources are easily accessible to the children, should they want to use them and do your best to accommodate any requests which you hadn't anticipated!
