Cubes cut into four pieces
Eight children each had a cube made from modelling clay. They cut them into four pieces which were all exactly the same shape and size. Whose pieces are the same? Can you decide who made each set?
Problem
Eight children sat round the big table at the end of the classroom. They each had a cube made from modelling clay.
"Cut your cube into four pieces which are all exactly the same shape and size," said their teacher, "and try to make your pieces different from everyone else's!"
When the children had cut the cubes up they put some of the pieces on the table in two rows with their names by them.
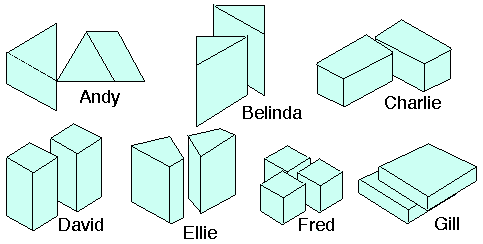
For accessibility: Andy has cut his cube into triangular prisms. Belinda has cut her cube into taller triangular prisms. Charlie and David have cut their cubes into cuboids. Gill has cut her cube into flatter cuboids. Ellie has cut her cube into irregular quadrilateral-shaped prisms. Fred has cut his cube into smaller cubes.
"Someone didn't cut theirs into four!" said Belinda pointedly.
Who was that and how many pieces were there?
"Two of us have made the same shapes," noticed Charlie.
Who were they?
Here are six cubes showing the way the children cut them.
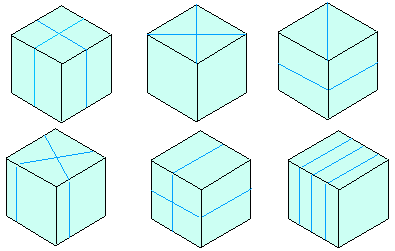
For accessibility: 6 cubes each with lines on them showing how they were cut. The first shows 2 cuts on the top face meeting at right angles down the middle of the sides of the cube. The second shows 2 cuts meeting at right angles going through each corner of the cube. The third shows a diagonal cut going through two corners of the cube on one face and, on the face next to it, a cut doing through the middle of the side of the face. The fourth shows two cuts going through points, which are not the corners nor the middle of the side, on one face of the cube. The fifth shows 2 cuts on a side face meeting at right angles down the middle of the sides of the cube. The sixth cube shows 3 equally spaced cuts which are parallel to each other on the top face of the cube.
Whose are they?
Getting Started
It might help to make some cubes out of modelling clay or plasticene and to cut them in the ways drawn.
Can you picture what shape the pieces will be when each cube is cut?
Student Solutions
Alistair sent us a very clearly-explained solution to this problem:
Fred did not cut his into four pieces, because it is the same as Charlie and David's only cut again, which means that he had eight pieces.
I have spotted that David and Charlie both cut their cubes into cuboids.
The six cubes shown were cut by: David, Belinda, Andy, Ellie, Charlie and Gill.
Thank you Alistair!
Well done too to Wafa from Jinnah Academy, Natalya from Seaton Primary, Vittal from Birchland and Samuel from Truscott Street Public School who all sent in very full solutions.
Teachers' Resources
Cubes Cut Into Four Pieces
Eight children sat round the big table at the end of the classroom. They each had a cube made from modelling clay.
"Cut your cube into four pieces which are all exactly the same shape and size," said their teacher, "and try to make your pieces different from everyone else's!"
When the children had cut the cubes up they put some of the pieces on the table in two rows with their names by them.
"Someone didn't cut theirs into four!" said Belinda pointedly.
Who was that and how many pieces were there?
"Two of us have made the same shapes!" shouted Charlie.
Who were they?
Here are six cubes showing the way the children cut them.
Whose are they?
Why do this problem?
This problem requires some visualisation, and knowledge of 3D shapes. It gives children experience of identifying shapes from pictures of them in different positions and orientations.
Possible approach
Key questions
Possible extension
Learners could try different ways of cutting cubes into more than four pieces, and draw the results.
Possible support
Having modelling clay cubes available for the children to cut in the ways drawn will help them access this problem.