The bridges of Konigsberg
Investigate how networks can be used to solve a problem for the 18th Century inhabitants of Konigsberg.
Problem
Konigsberg (now called Kaliningrad) is a town which lies on both sides of the Pregel River, and there are also parts of the town on two large islands that lie in the river. In the 18th century the river banks and islands were connected with seven bridges (as shown below).
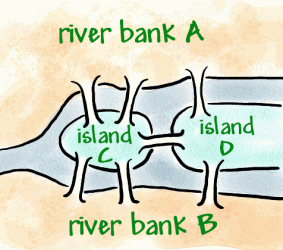
A popular problem of the time was whether or not it was possible to go for a walk around Konigsberg crossing each bridge exactly once.
Can you find a route around Konigsberg which crosses each bridge exactly once?
Here are two more questions:
- Can you remove a bridge and find a walk that crosses each remaining bridge exactly once?
- Can you add a bridge and find a walk that crosses all the bridges exactly once?
To simplify the problem, we can represent Konigsberg by a network of vertices and edges, where each vertex represents one of the land masses (the river banks and islands) and each edge represents a bridge.

Try adding another edge (bridge) between vertices A and D. Draw out this new network.
- Can you now find a route which uses each edge exactly once?
- Are there any restrictions on which vertex you can start from?
- Can you add one (or more) edges to the original network so that there is a walk which crosses every bridge exactly once, and where you finish at the same vertex where you started?
To find out more about when it is possible to travel along every edge of a network exactly once, try the problem "Can You Traverse It?".
You can read more about the Bridges of Konigsberg in this Maths In a Minute Plus article.
To find out how this problem developed into graph theory go to From Bridges to Networks Plus article.
Getting Started
Euler used a graph to explain the possible routes around Old Konisberg. He represented the land by dots and the bridges by lines joining the dots. Think about whether there is an even number of bridges or an odd number of bridges from each piece of land.
Student Solutions
We received three good solutions - two almost completely correct, fromYanqing from Lipson Community College and from Sarah from Colyton, and one completely correct from Andrei from Tudor Vianu College in Bucharest. Well done to you all.
Andrei's solution follows:
First, I observe that for the first figure it is impossible to cross each bridge once. This happens because you would remain in a place where all the bridges were already crossed.
In the second case, it is possible to cross the bridges only once and create a circuit.
I worked with different number of bridges and islands and I obtained solutions for each of the following:
- bridge traversing circuits
- bridge traversing paths
- Hamiltonian circuits
- Situations where none of the above is possible.
For 8 bridges I found:
- A diagram with a bridge traversing circuit.
The circuit is the following: S-C-A-D-B-A-C-B-S
- A diagram with a bridge traversing path:
The path is the following: S-D-E-A-B-S-C-E-B.
- A Hamiltonian circuit and a bridge traversing circuit:
- A diagram in which neither is possible. In the diagram below, neither a traversing path nor a traversing circuit is possible:
Editor's note:
If you were allowed to start at another island you could have a traversable path: starting at the top right hand island and finishing in the top left hand island, or vice versa.
Teachers' Resources
Students could also watch "Bridges of Königsberg: The Movie"!
