Hamilton's puzzle
Problem
In 1859, the Irish mathematician Sir William Rowan Hamilton devised a puzzle with a regular dodecahedron made of wood. Here is a dodecahedron:
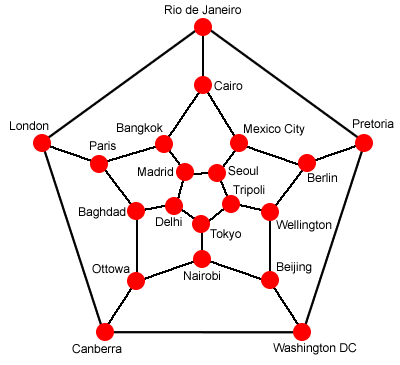
He labelled each of the vertices with the name of an important city. The challenge was to find a route along the edges of the dodecahedron which visited every city exactly once and returned to the start.
Here is a graph which represents the dodecahedron. Can you see how each of the 20 vertices, 30 edges and 12 pentagonal faces is represented in the graph?
I start my journey in Rio de Janeiro and visit all the cities as Hamilton described, passing through Canberra before Madrid, and then returning to Rio. What route could I have taken?
Can you find any other ways of making this journey?
Here is a simpler network of countries:
How many different ways are there of visiting each of these countries once and only once, beginning and ending at Australia?
Getting Started
From Rio, where could you go next? Can you find a route using each of these second stops?
Starting at Australia, where can you go next? Can you choose one of these second countries and decide what the possibilities are now?
Might it help to record the routes?
How will you make sure you have found them all?
Student Solutions
Thomas from New York sent in a very clear solution to the Hamiltonian problem. He wrote:
One route around the dodecahedron is: Rio, Pretoria, Washington
DC, Canberra, London, Paris, Baghdad, Ottawa, Nairobi, Beijing,
Wellington, Berlin, Mexico City, Seoul, Tripoli, Tokyo, Delhi,
Madrid, Bangkok, Cairo, Rio.
There are other routes, such as: Rio, London, Canberra, Washington
DC, Pretoria, Berlin, Wellington, Beijing, Nairobi, Ottawa,
Baghdad, Paris, Bangkok, Madrid, Delhi, Tokyo, Tripoli, Seoul,
Mexico City, Cairo, Rio.
Other solutions were sent in by Thomas from Heversham St Peter's Primary School, Michael from North Sydney Boys High School and Katherine from The Hills Grammar School. These included:
Rio de Janeiro to London to Canberra to Ottowa to Nairobi to
Beijing to Washington DC to Pretoria to Berlin to Wellington to
Tripoli to Tokyo to Delhi to Baghdad to Paris to Bangkok to Madrid
to Seoul to Mexico City to Cairo and back to Rio de Janeiro.
1. Rio de Janeiro 2. Cairo 3. Mexico City 4. Berlin 5. Pretoria 6.
Washington DC 7. Canberra 8. Ottowa 9. Baghdad 10. Delhi 11. Tokyo
12. Nairobi 13. Beijing 14. Wellington 15. Tripoli 16. Seoul 17.
Madrid 18. Bangkok 19. Paris 20. London 21. Rio de Janeiro
Rio de Janeiro to Pretoria to Washington D.C. to Canberra to Ottowa
to Nairobi to Beijing to Wellington to Berlin to Mexico City to
Cairo to Bangkok to Madrid to Seoul to Tripoli to Tokyo to Dehli to
Baghdad to Paris and then back to Rio de Janeiro.
You will have realised that there are many, many more than this -
but thank you to all those of you who sent in some solutions.
Thomas from New York was the only one to go on to the second part
of the question. Well done Thomas for persevering! He says: