Coordinate Patterns
Charlie and Alison have been drawing patterns on coordinate grids. Can you picture where the patterns lead?
Problem
Coordinate Patterns printable worksheet
Charlie and Alison have been drawing patterns on coordinate grids. You may want to choose just one to explore or you may like to try all three.
Charlie's Squares
Charlie has been drawing squares.
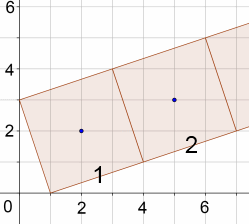
What will the coordinates of the centre of square number 3 be?
How do you know?
Charlie wants to know where the centre of square number 20 will be.
Can you use the diagram above to help you to work this out?
Can you suggest a quick and efficient strategy for working out the coordinates of the centre of any square?
Would your strategy work if Charlie's sequence extended to the left? $$\ldots, -2, -1, 0, 1, 2, 3, \ldots$$
Can you adapt your strategy to work out the coordinates of the corners of any square? How would you explain your new strategy to someone else and convince them that it would work for any square?
Alison's Triangles
Alison has been drawing triangles.
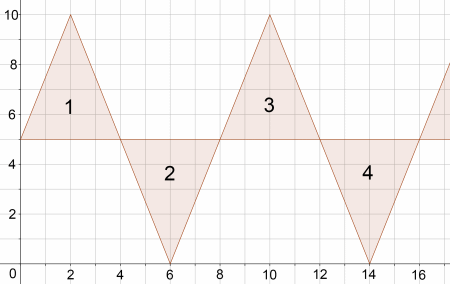
She wants to know where the vertices of triangle number 23 will be.
Can you use the diagram to work it out?
Can you suggest a quick and efficient strategy for working out the coordinates of the vertices of any triangle?
Would your strategy work if Alison's sequence extended to the left? $$\ldots,-2, -1, 0, 1, 2, 3, \ldots$$
How would you explain your strategy to someone else and convince them that it would still work?
More Squares from Charlie
Charlie has been drawing more squares.
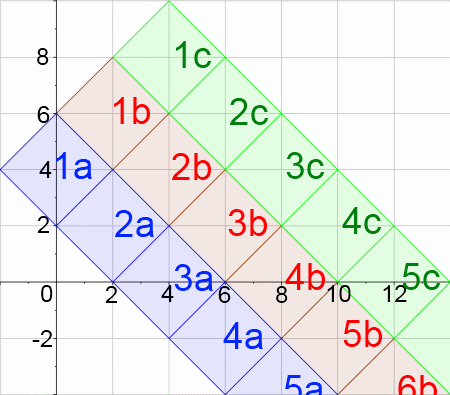
He wants to know what the coordinates of the centre of square 22b will be.
Can you use the diagram to work it out?
Can you suggest a quick and efficient strategy for working out the coordinates of the vertices of any square?
How would you explain your strategy to someone else and convince them that it would work for any square?
You may have found one strategy in each case, or more than one. Compare your strategies with those that other students have found. What's the same and what's different?
Try making your own coordinate pattern. What questions could you ask about your pattern? Is there an efficient strategy that someone could use to answer these questions?
Getting Started
How do you move from one square to the next?
What do you notice about the x coordinates of the centres?
What do you notice about the y coordinates of the centres?
Student Solutions
Wow, we received loads of solutions here! Let's have a look at a few of them:
Charlie's Squares
William and Chris, from Croftlands Junior School, tried to approach Charlie's Squares this way:
We found that the best way to organise our information was to draw a table. Here is the table we drew:
| Square | x-coordinate | y-coordinate |
| 1 | 2 | 2 |
| 2 | 5 | 3 |
| 3 | 8 | 4 |
| 4 | 11 | 5 |
| 5 | 14 | 6 |
Using the table, we found out that the x-coordinate was going up 3 every time. We added a couple of extra examples in the table. We spotted that the y-coordinate was the number of the square plus 1. Then we tried spotting patterns by working with the y coordinates to find the x coordinates.
A great way to start! They then went on to find the general formula correctly. Callum, Elys, Cerys, Elgan, Cullen, Ethan, Ifan and Twm, from Ysgol Llanegryn, jumped straight in with the following:
We first found a pattern: (2,2), (5,3), (8,4), and we then discussed how to find any centre square. We turned to algebra. The nth term in the pattern is (3n -1, n + 1) so the coordinates of the 20th centre point would be (60-1, 20+1) which is (59,21).
Justin, from the John of Gaunt School, correctly noted:
In the case of going to the left, the process is repeated but instead of increasing the horizontal and vertical coordinates, the coordinates decrease by the same amounts.
Sam, from Fern Avenue, gave the following answer to Alison's Triangles:
I started by comparing triangles 1 and 3, and realised that 'middle' vertices on nearby odd triangles were exactly 8 points horizontally apart. That, with the fact that all odd middle vertices have coordinates of the form (x,10), allows you to find the middle vertex of any odd numbered triangle.
The same applies for all even numbered triangles, except that the vertices are on coordinates that are 4 grid squares to the right of the odd triangles.
After noticing this, I realised that the even isosceles triangles continued to the middle vertex of the odd numbered triangles, and vice-versa. This meant that they either went down or up 5 squares, and right 2 squares.
I now realised that if I knew the coordinates of any triangle, then I knew the middle vertex of the next triangle.
Therefore, triangle 23 will have vertices at (88,5), (90,10), and (92,5).
Joe and Jack, from Springfield Primary School, gave us their formula for the x-coordinate of the top/bottom vertex of the nth triangle, which was 4n-2. From this they plugged in n = 23, which gave them the correct x-coordinate, and noticed that the y-coordinate alternates between 10 (when n was odd) and 0 (when n was even). Great!
More Squares from Charlie
Penny, Jacob, Patrick and Cameron, from Inter Lakes, submitted solutions to More Squares from Charlie. Cameron wrote:
The coordinates of the centre of square 22b are (44,-36). To work this out, first I made a chart for the x-coordinates and the y-coordinates. To get from one 'b' square to the next, add 2 to the x-coordinate and subtract 2 from the y-coordinate. My quick and efficient strategy is knowing the x and y axis rules.
Brilliant!
A recap of rules for the nth term
Like some of the students featured above, Ivan Ivanov from the 47th High School in Sofia, Bulgaria put his reasoning into algebraic form. He found formulas for the coordinates of the shapes using the nice notation below. Well done to everyone who found similar formulae.
Charlie's Squares
- If $C(n)$ is the centre of square $n$,
then the coordinates of $C(n)$ satisfy the equations: $x(n) = 3n - 1$, and $y(n) = n + 1$. - If $L(n)$ is the bottom left hand vertex of square $n$,
then the coordinates of $L(n)$ satisfy the equations: $x(n) = 3n - 2$, and $y(n) = n - 1$.
These formulas both give the correct coordinates even when Charlie goes left with values $n = ....-2, -1, 0, 1, 2, 3....$.
Alison's Triangles
- If $C(n)$ is the top or bottom vertex of triangle $n$ (for odd and even $n$ respectively), then the coordinates of $C(n)$ satisfy the equations: $x(n) = 4n - 2$, $y(n) = 10$ when $n$ is odd and $y(n) = 0$ when $n$ is even.
- If $L(n)$ is the left-most vertex of triangle $n$, then the coordinates of $L(n)$ satisfy the equations: $x(n) = 4n - 4$, $y(n) = 5$.
- The right-most vertex of triangle $n$ is the same as the left-most vertex of triangle $n-1$.
Again, these formulas give the correct coordinates when Alison works left with values $n = ....-2, -1, 0, 1, 2, 3....$.
More Squares from Charlie
If $B(n)$ is the centre of square $nb$, then the coordinates of $B(n)$ satisfy the equations: $x(n) = 2n$, and $y(n)B = -2n + 8$.
You might like to think if you can find a formula for squares such as 19c or 199a. What about if Charlie continues the pattern and draws squares such as 1d and 1e, etc?
Michael Sena from NSBH sent in a little computer program that could give the coordinates of any of Charlie's first set of squares, even producing a table of the first few. Well done!
Thanks again to everyone for their solutions!
Teachers' Resources
Why do this problem?
This problem offers a good opportunity for students to discuss patterns and find convincing arguments for their solutions.
Reuben Hersh has written that:
"In the classroom, convincing is no problem. Students are too easily convinced. Two special cases will do it."
This problem offers an opportunity to ensure that students are justified in generalising from the particular cases that they have selected.
Possible approach
These printable resources may be useful: Coordinate Patterns (worksheet),
Coordinate Patterns (diagrams).
Show the first diagram. It's available as a PowerPoint, or you could print out the worksheet.
"I wonder if you can now work out the coordinates of the centre of square number 20 from the image, without working out the centres of the squares in between."
Bring the class together and invite those students with interesting or elegant strategies to present their ideas to the rest of the class.
Possible support
Before working on this problem students could develop fluency in using coordinates by working on Treasure hunt and fluency with linear sequences by taking a look at Shifting times tables.
Possible extension
Find a general symbolic expression for the coordinates of the vertices of the $n$th square or triangle.
