Circle Scaling
Problem
You are given a circle with centre O. Describe how to construct with a straight edge and a pair of compasses, two other circles centre O so that the three circles have areas in the ratio 1:2:3.
Getting Started
If the areas are in the ratio 1:2:3 what can you say about the ratio of the radii?
Can you find some key right-angled triangles that will give you the lengths you are after? Pythagoras' theorem is useful!
Some useful constructions can be found in the Thesaurus if you look up "construction". A perpendicular line might be particularly useful.
Student Solutions
Many thanks to Junwei of BHASVIC school for the basis of this solution. A solution was also received from Andrei of School 205, Bucharest.
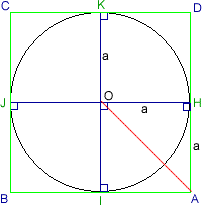
First draw a circle, centre O and radius of a.
Draw two diameter lines inside the circle, and make sure these two lines are perpendicular.
From these two lines, we can draw four tangents to the circle which form a square ABCD touching the circle at HIJK.
Then OH = a = HA.
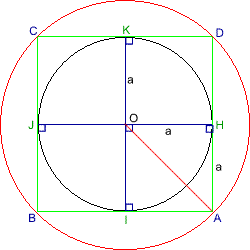
Thus, OA equals $a\surd 2$.
Using the compasses with focus on O and length OA, make another circle which has an area two times the area of the original circle.
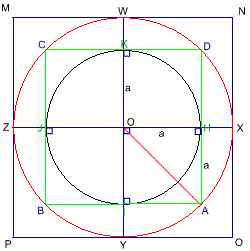
Extend the original diameter lines to be the diameter lines for the new circle, and use the same method to form a new square MNOP which touches the new circle on WXYZ.
Thus,$OZ =a\surd 2. $
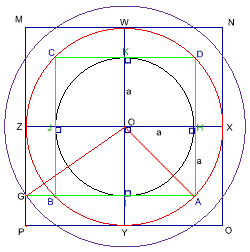
Then extend AB to touch the bigger square's side PM on G. Since $OG^2 = OZ^2 + ZG^2 = 3a^2$, then $OG = a \sqrt 3.$ Using the circle area formula, with radii of the three circles a, $a \sqrt 2$ and $a\sqrt 3$ respectively, we can easily work out that the ratio of their areas is 1:2:3.
Teachers' Resources
This is delightfully simple once you spot the way to do it, a real 'aha' question!
