Flower
Problem
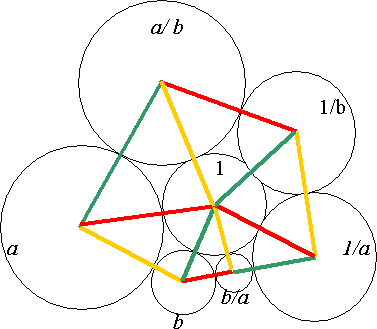
You are given a circle of radius 1 unit and two circles of radius $a$ and $b$ which touch each other and also touch the unit circle. Prove that you can always draw a 'flower' with six petals (as in the sketch) with the unit circle in the middle, and six circles around it having radii $a$, $b$, $b/a$, $1/a$, $1/b$ and $a/b$, such that each outer circle touches the unit circle and the two circles on either side of it.
[Note: this diagram is not drawn accurately. Drawing your own more accurate diagram may help you to do the question.]
Getting Started
You need to use the fact that if two circles touch then the line joining their centres goes through the point at which they touch. (Why is that?) Then join the centres of all the 'petals' to the centre of the inner circle and draw the hexagon formed by joining the centres of adjacent 'petals' as in the sketch. After that the proof depends on finding similar triangles.
Student Solutions
I denoted by $A$ the centre of the circle of radius $a/b$, by $B$ the centre of the radius $a$, by $C$ the circle of radius $b$, by $D$ the centre of the circle of radius $b/a$, by $E$ the centre of the circle of radius $1$/a, by $F$ the centre of the circle of radius $1/b$ and by $O$ the centre of the circle of radius 1.
I observed that the triangles obtained have the following sides:
| ABO | a/b + a | a +1 | a/b +1 |
| BCO | a + b | a + 1 | b + 1 |
| CDO | b + b/a | b + 1 | b/a + 1 |
| DEO | b/a + 1/a | b/a + 1 | 1/a + 1 |
| EFA | 1/a +1/b | 1 + 1/b | 1 + 1/a |
| FAO | a/b + 1/b | a/b + 1 | 1/b + 1 |
I observe that triangles $BCO$, $DEO$ and $FAO$ are similar, with the similarity ratios (taking them two by two), $1: 1/a: 1/b$ respectively. So are triangles $ABO$, $CDO$ and $EFA$, with the similarity ratios $a: b: 1$.
Looking in the similarity ratio, I observe that angle $BOC$ is congruent with angle $DEO$ and with angle $AFO$, angle $OBC$ with angles $FAO$ and $EOD$, and angle $BCO$ with $ODE$ and $AOF$.
This means the sum of angles $BOC$, $AOF$ and $DOE$ is the angle sum in a triangle, i.e. $180^0$.
For triangles $AOB$, $COD$ and $EOF$ that are similar, angles $AOB$, $ODC$ and $OEF$ are congruent; so are angles $OAB$, $OFE$ and $DOC$ and $ABO$, $OCD$ and $FOE$. In this case the sum of angles: $AOB$, $COD$ and $EOF$ is $180^0$.
So, the sum of all angles around point O is $360^0$. This means that, with the given radii, it is always possible to construct such a flower.
Teachers' Resources
The proof depends on identifying two sets of similar triangles and spotting that they are arranged around the centre of the inner circle in such a way that they can be used to show that they fit together exactly as the angles add up to 360 degrees. The method is elementary but calls for a systematic approach.
