Lunar angles
Problem

The angle between two circles at the point of intersection is the angle between the tangents to the circles at that point contained in the overlapping area or lune. Prove that, for any two circles, the angles at both points of intersection are equal.
Three circles intersect at the point $D$ and, in pairs, at the points $A,\ B$ and $C$ so that the arcs $AB$, $BC$ and $CA$ form a curvilinear triangle with interior angles $\alpha$, $\beta$ and $\gamma$ respectively. The diagrams show two possible cases. Prove that, for any three such circles, $\alpha + \beta + \gamma = \pi$.


When you have done this question you might like to consider what happens on the surface of a sphere where instead of a flat surface (Euclidean geometry) you are working on a surface with positive curvature (Spherical or Elliptic geometry). See the article
Getting Started
Look for equal angles and angles on a straight line.
Student Solutions
I divided the solution into two parts: the demonstration of the congruence of angles, and the demonstration that the three angles add up to $180^o$.
1. Congruence of angles in a lune
Let $O_1$ and $O_2$ be the centres of two circles, $A$ and $B$ the intersection points and $M$ and $N$ the intersections of the tangents to these two circles. I observed that triangles $O_1AO_2$ and $O_1BO_2$ are congruent, because they have a common side $O_1O_2$, and the other two sides are radii in the two circles. So, angle $O_1AO_2$ and $O_1BO_2$ are equal to say $\theta$. A tangent to a circle and the radius to the point of contact are perpendicular so $\angle MAO_2 = \angle NAO_1 =\angle MBO_2 = \angle NBO_1 = 90^o$. Hence $\angle O_1AM = \angle O_2AN =\angle O_1BM =\angle = \angle O_2BAN = \theta - 90^o$. So, $\angle MAN = \angle MBN$.
2. Let $O_1$, $O_2$ and $O_3$ be the centres of the three circles respectively, D the point common to all three circles, and $T_1T_1'$, $T_2T_2'$, $T_3T_3'$ the three tangents. In my figure the radius and the tangent to circle 1 are in red, to circle 2 in blue and to circle 3 in green respectively.
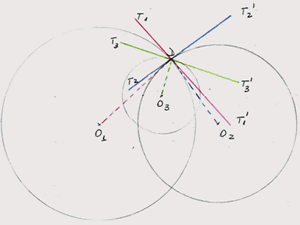
From the previous point, I see that angle $\alpha$ has the same measure with angle $T_2DT_1'$ and to the angle $T_1DT_2'$ (the last two being vertically opposite angles).
In the same manner I found: $\beta = \angle T_1'DT_3' =\angle T_1DT_3$ and $\gamma = \angle T_3DT_2 = \angle T_3'DT2'$. \par This way, it is easy to see that the three angles add up to $180^o$: $\alpha + \beta + \gamma = T_2DT_1' + T_1'DT_3' + T_3'DT_2' = T_2DT_2' = 180^o$. \par For the second case, I follow exactly the same steps.
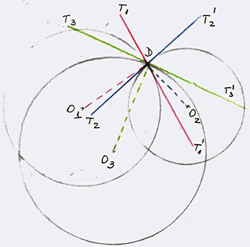
I find $\alpha = \angle T_2DT_1'$, $\beta = \angle T_2'DT_3' = \angle T_2DT_3$ and $\gamma \angle T_3DT_1 = \angle T_3'DT_1'$.
The result is the same, i.e. that in this case the three angles add up to $180^o$ again.
Teachers' Resources
Although this is an unusual question it is very straightforward and depends only on understanding that the angle between two curves is the same as the angle between their tangents at the point of intersection. This is good preparation for an introduction to non-Euclidean geometry.
