Tricky Track
In this game you throw two dice and find their total, then move the appropriate counter to the right. Which counter reaches the purple box first?
Problem
You need twelve counters and two ordinary $1$-$6$ dice for this activity.
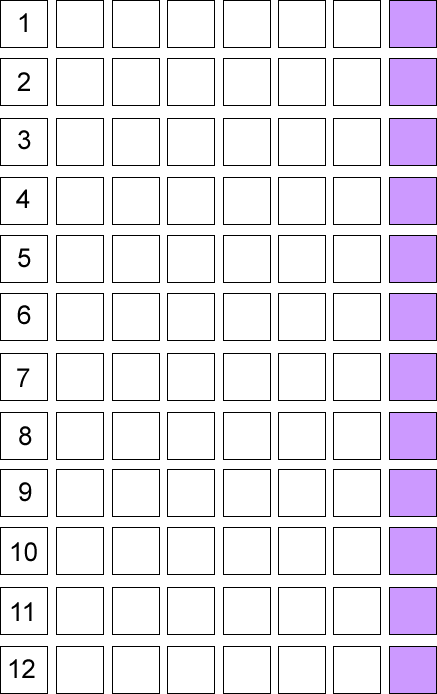
Draw out a board like this (you may find that squared paper is useful!):
Or, you can print it off here: pdf .
RULES
Place one of the twelve counters on each of the squares numbered $1$ to $12$.
Roll the dice and add together the two numbers shown.
Move the counter on that numbered square one box to the right.
Now roll the dice again and repeat this, each time moving the counter on that "row" one box to the right.
Which counter reaches the purple box first?
Is this what you would expect?
Play a few more times and make a note of which counter reaches the end of its row first.
Can you explain why you get these results?
Getting Started
How can you get a total of $1$ ... $2$ ... $3$ etc?
Are you sure you have found all the ways of getting that total?
How will you record what you're doing?
You may find it useful to use two differently coloured dice.
Student Solutions
Jacob from Fern Avenue Public School thought carefully about this problem:
To figure out the counter that wins most often, we first need to figure out the most common dice rolls.
There are $36$ different possible combinations. Here they are, in the format "First Die Roll - Second Die Roll - Total":
$1 - 1 - 2$
$1 - 2 - 3$
$1 - 3 - 4$
$1 - 4 - 5$
$1 - 5 - 6$
$1 - 6 - 7$
$2 - 1 - 3$
$2 - 2 - 4$
$2 - 3 - 5$
$2 - 4 - 6$
$2 - 5 - 7$
$2 - 6 - 8$
$3 - 1 - 4$
$3 - 2 - 5$
$3 - 3 - 6$
$3 - 4 - 7$
$3 - 5 - 8$
$3 - 6 - 9$
$4 - 1 - 5$
$4 - 2 - 6$
$4 - 3 - 7$
$4 - 4 - 8$
$4 - 5 - 9$
$4 - 6 - 10$
$5 - 1 - 6$
$5 - 2 - 7$
$5 - 3 - 8$
$5 - 4 - 9$
$5 - 5 - 10$
$5 - 6 - 11$
$6 - 1 - 7$
$6 - 2 - 8$
$6 - 3 - 9$
$6 - 4 - 10$
$6 - 5 - 11$
$6 - 6 - 12$
Number of appearances of $2$: $1$
Number of appearances of $3$: $2$
Number of appearances of $4$: $3$
Number of appearances of $5$: $4$
Number of appearances of $6$: $5$
Number of appearances of $7$: $6$
Number of appearances of $8$: $5$
Number of appearances of $9$: $4$
Number of appearances of $10$: $3$
Number of appearances of $11$: $2$
Number of appearances of $12$: $1$
Looking at all of the totals, we can see that $2$ appears once, $3$ twice, $4$ thrice, and so on until we get to $7$. At this point, the number of appearances starts to decrease. $8$ appears five times, $9$ four, and $12$ only once. We can see that $7$ appears most often, and is therefore most likely to win the race.
But why does $7$ appear most often? It is because there is no result for the first die rolled that excludes it as a result. If you look back at the table, you can see that no matter what is rolled on the first die, seven still has a $1$ in $6$ chance of being the result. This is not true for any other number. And this is why $7$ is the most common result.
What if the dice had seven faces? $7$ would no longer be the most common number, as a roll of $7$ on the first die would eliminate it as a result. Instead, $8$ is the most common, for the reasons mentioned above. If the dice had eight faces, then $9$ would be the most common. There is a pattern here: if two dice are being rolled, the most common result can be determined by adding $1$ to the number of faces each die has.
Very well done, Jacob. Here is another way to display the possible totals when rolling two $1-6$ dice:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
