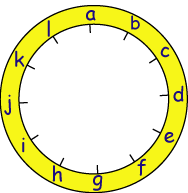
A Mixed-up Clock

There is a clock-face where the numbers have become all mixed up. Can you find out where all the numbers have got to from the ten statements below?

Here is a clock-face with letters to mark the position of the numbers so that the statements are easier to read and to follow.

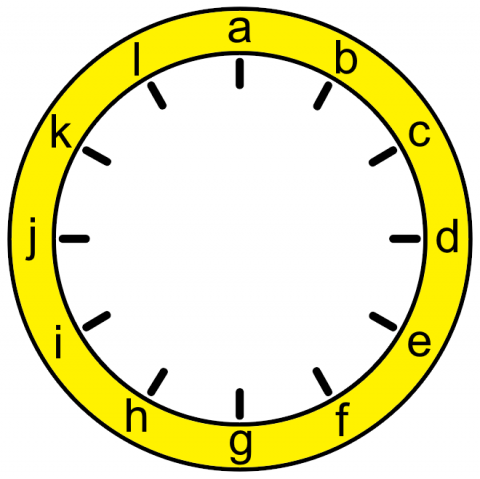
1. No even number is between two odd numbers.
2. No consecutive numbers are next to each other.
3. The numbers on the vertical axis (a) and (g) add to $13$.
4. The numbers on the horizontal axis (d) and (j) also add to $13$.
5. The first set of $6$ numbers [(a) - (f)] add to the same total as the second set of $6$ numbers [(g) - (l)] .
6. The number at position (f) is in the correct position on the clock-face.
7. The number at position (d) is double the number at position (h).
8. There is a difference of $6$ between the number at position (g) and the number preceding it (f).
9. The number at position (l) is twice the top number (a), one third of the number at position (d) and half of the number at position (e).
10. The number at position (d) is $4$ times one of the numbers adjacent (next) to it.