The Deca Tree
Find out what a Deca Tree is and then work out how many leaves there will be after the woodcutter has cut off a trunk, a branch, a twig and a leaf.
Problem
In the forest there is a Deca Tree.
A Deca Tree has 10 trunks,

and on each trunk there are 10 branches,

and on each branch there are 10 twigs,

and on each twig there are 10 leaves:

One day a woodcutter came along and cut down one trunk from the tree.
Then he cut off one branch from another trunk of the tree.
Then he cut off one twig from another branch.
Finally he pulled one leaf from another twig.
How many leaves were left on the tree then?
How did you work out the solution?
Getting Started
How many leaves are there on ten twigs?
How many leaves did the Deca Tree have before the woodcutter came along?
How many leaves did the woodcutter chop off each time?
Student Solutions
Thank you to everybody who sent in their solutions to this problem. We had lots of detailed explanations sent in.
Pei Lin from Scotholme Primary School in England found the total number of leaves and then subtracted each number separately:
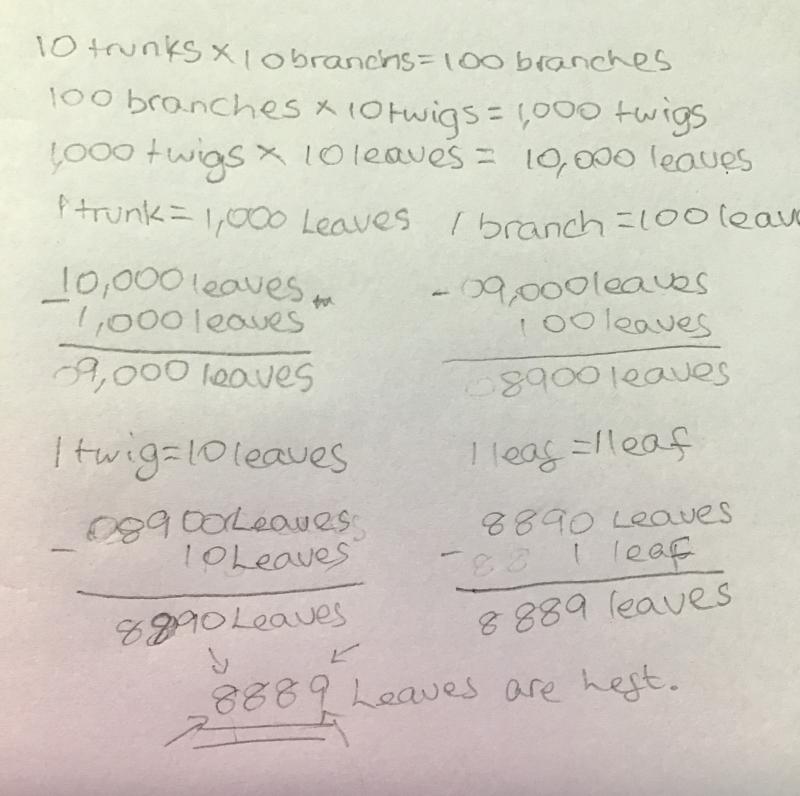
Thank you for showing us how you worked this out. James from Hamstel Junior School in England found the solution by working out how much to subtract in one go:
The woodcutter removes:
1 trunk = 1000 leaves
1 branch = 100 leaves
1 twig = 10 leaves
1 leaf = 1 leaf
This means the woodcutter removes 1,111 leaves in total.
Well done, James!
We had lots of other solutions sent in that were very similar to either Pei Lin's solution or James' solution. Thank you to the following children for their clear explanations: Sandra from Belgium; Dylan from the UK; Humphrey from Twyford School in England; Anna, Serenade, Akira, Maddox and Kenny from Sahuaro Elementary in the USA; K from Crossflatts Primary School in the UK; Elliot from Haddington Primary School in the UK; Penny from Hillbrook Primary School in the UK; Isla Eve from Walton and Holymoorside Primary School in the UK; and Parker from JPSS in Australia.
James also used the phrase 'power of 4' to describe multiplying ten by itself four times:
The total number of leaves on the complete Deca Tree is 10 to the power of 4 which equals 10,000 leaves.
This is a quick way of working out the number of leaves on the original tree - well done!
Teachers' Resources
Why do this problem?
The problem can also help children to appreciate how big large numbers really are!
Possible approach
You could introduce the problem by telling the class the 'story' about the tree and its trunks, its branches, its twig and its leaves. You may wish to show the group the images in the problem, or you could create your own on the board as you outline what a Deca Tree looks like.
Key questions
Might a picture help?
If there are ten twigs on each branch, how many will there be on ten branches?
How many leaves are there on ten twigs?
How many leaves did the Deca Tree have before the woodcutter came along?
How many leaves did the woodcutter chop off each time?
Possible support
In addition to, or instead of, drawing sketches, it might help some children to make a model of part of the tree. Pipecleaners could work well for this purpose.
Possible extension
Children could be invited to invent a similar tree with different numbers of branches etc., such as a five-branched 'Penta' tree or an eight-branched 'Octa' tree.
