Trebling
Can you replace the letters with numbers? Is there only one solution in each case?
Problem
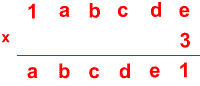

Can you replace the letters with numbers? Is there only one solution in each case?
Once you've had a chance to think about it, click below to see how two different pupils began working on the task.
Here is Abdullah's work:
"For each problem I first looked to find a number that would make the ones column accurate, then I substituted the number for the answer in the tens column and then continued the process until the calculation was complete."
Joshua wrote:
"I wrote out single digit multiples of three up to 9 because each letter was one digit. I noticed that the numbers 1 to 9 only appeared once in the ones column of the answers. I looked at the question and realised that 3 x e had to be 21 because it was the only answer ending in 1. This meant that e had to be 7.
I carried the 2 and took it from 7 (the other e) and got 5. So d x 3 had to end in 5 which meant d had to be 5 because 5 x 3 = 15. I then repeated the process."
Can you take each of these starting ideas and develop it into a solution?
Getting Started
Would it help to start by looking at the units column when multiplied by $3$?
Don't forget that the digits appear in the answer too!
Student Solutions
We received a lot of solutions to this task, so thank you to everybody who sent us their thoughts. We've focused here on the solutions where children explained how they approached solving the problem.
Millie explained how they started to approach this problem:
I started with (blank)1 divided by 3 is what? and came up with 21 divided by 3 is 7. I repeated this method with the other numbers, replacing the letters as I went along until I finished the puzzle.
Good idea, Millie! This problem might look very difficult to solve at first, but starting on the right and using the fact that the answer must end in 1 gives you a way in.
Lots of children from Highgate School in the UK sent us their solutions to this problem - thank you all for your hard work! Everybody used the same general idea of starting with the ones column (also referred to by some children as the 'units column'). CS said:
For both of the calculations, I worked out the units, like ‘j x 3’ and the answer ends in 2, so I know that j should be 4, because 3 x 4 = 12, and you carry the one into the next column. Later on, unravelling the question is much easier because I have solved what the letters actually mean. You can just repeat the same steps and see if it is correct by doing the inverse operation.
Olivia said:
I worked from right to left. The first digit had to be 7 because 7×3 is 21 and that ends in 1. I carried the 2 and then I had to look for a number which when multiplied by 3 with 2 added gives a number with 7 in the last digit. I continued doing this from right to left until I had found all the numbers.
Lion gave the full solution along with an explanation of their technique:
I have solved the Trebling problem and these are my answers:
a=4
b=2
c=8
d=5
e=7
f=8
g=5
h=7
i=1
j=4
I solved this problem by looking at the units digit and seeing what in the 3 times table could make that e.g 3x?=?1(in that case 7). I did this all throughout the problem and was successful.
P.S: If you carry anything, you subtract that number from your units digit e.g. 3x?=?8 if a two is what you carry, you do 8-2 so 3x?=?6.
Vaughan said:
I started by writing the three times table. Then, I noticed that in the units column of the three times table answers, each number 1-9 only appeared once. I started at the right hand side of the calculation, and used the number in the units column of the solution to back-calculate what the figure in the units column of the number being multiplied was. Then I carried over the number in the tens column of the answer to the three times table, into the next column. Then I took that away from the number I had just solved in the code to work out what number needs to be in the units column of the next three times table answer. I did that repeatedly until the calculation was solved.
Thank you all for sharing your techniques with us. Lots of children talked about the importance of considering the number that is 'carried' into the next column. In some schools, children might think of this as a number being 'exchanged' instead.
Vaughan has noticed something interesting - each number from 1-9 only appears once in the ones column of the three times table up to 30. I wonder if this problem would have needed a different approach if we had focused on a different times table, such as the five times table?
Well done to the following children who also sent in some excellent explanations of their techniques for solving this problem: Tom, Adi, Zaki, Lottie, Soha, Louis, Alyssa, Rishaan, Henry, Eloise, Silas, Katie, Emilia, Gabriel, Jane, Savva and Jesse from Highgate School; Kyra from the UK; and Tzi Ying.
Some children sent in a more detailed explanation of how they found several steps of the solution of the first problem. The following solutions are from children at Highgate School.
Monty said:
I worked out that for the units in the answer to be 1, the units in the top row must be 7 (3x7=21). Now that I knew that e=7, I could work out that the tens column in the top row must be 5 (3x5=15 plus the 2 that I carried from 21 = 17). The same logic for the other columns helped me work out the other numbers (3x8 + 1 = 25), (3x2=6), (3x4=12), (3x1 + 1 = 4).
William sent in this picture with the full solution, which can be clicked on to make it bigger:

Isla sent us this very clear explanation:
To solve this problem I started with the first column which had an e in it. I knew that we were multiplying by 3 so I asked myself ‘what multiplied by 3 gets you a number that ends with a 1’ I came to the conclusion that e could be 7 as 7x3 gives us 21 which ends with a 1. Now after this I moved onto the next column. In the next column I knew that there would be a carry of 2 from the first column. So, I then asked myself what 3 multiplied by something add 2 would be. However, I noticed in the answer box there is an e which in the last column I thought would be 7 so this means that the number in the second column would end in a 7. Then I thought about what the closest number in the 3 times table to a number that ends in a 7. I concluded that d = 5 as [3x5] +2 would get you 17 which is a number that ends in 7. Then I moved onto the 3rd column. There was a d in the answer column which means that the 3rd column answer is going to end in a 5 as d=5. We also have a remainder from the 17. So I had to ask myself ‘what multiplied by 3 add 1 gets me an answer that ends with a 5’. I instantly thought of 25 seeing as c could be an 8. First, I tested out if c could be 8 by multiplying 3x8 and then adding 1 which gives me 25 which is a number that ends with a 5 so that would work. After this I continued this method until I solved the problem.
Top Tip
It helps to add a key as then you don’t forget what the letters are as numbers!
Good tip, Isla! All of these explanations show clearly how we can develop Joshua's idea from the main task into a full solution.
We were also sent solutions by a lot of different children at the British School of Beijing in Shunyi, China. The following pictures can be clicked on to make them bigger. Max and Daniel sent in this picture of their solution:

Alice, Mary, Tiffany and Hui Ling sent in the following picture:

Thank you all for sending in these ideas! Thank you as well to Iyla and Noah from England and Milo and Jett from Highgate School who also sent us clear explanations of how they solved this problem.
Teachers' Resources
Why do this problem?
Possible approach
Allow at least fifteen minutes for a final discussion. Invite some pairs to explain how the two different methods might be continued. You may find that some members of the class used completely different approaches when they worked on the task to begin with, so ask them to share their methods too. You can then facilitate a discussion about the advantages and disadvantages of each. Which way would they choose to use if they were presented with a similar task in the future? Why?
Key questions
Possible extension
Possible support
