ArRh!
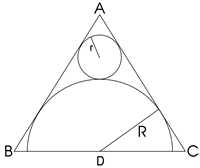
Triangle ABC is equilateral. D, the midpoint of BC, is the centre of the semi-circle whose radius is R which touches AB and AC, as well as a smaller circle with radius r which also touches AB and AC. What is the value of r/R?
Problem
Triangle ABC is equilateral. D, the midpoint of BC, is the centre of the semi-circle whose radius is R which touches AB and AC, as well as a smaller circle with radius r which also touches AB and AC.
What is the value of ${\bf \frac{r}{R}}$?
Student Solutions
This is really an 'aha' problem: the sort that has a very short and sweet solution, if you look at it the right way. We leave this as a further challenge for you to think about and send your ideas to 'Further Inspirations'. We give the solution sent by David of Madras College, St Andrews which depends on splitting the equilateral triangle into four smaller equilateral triangles.
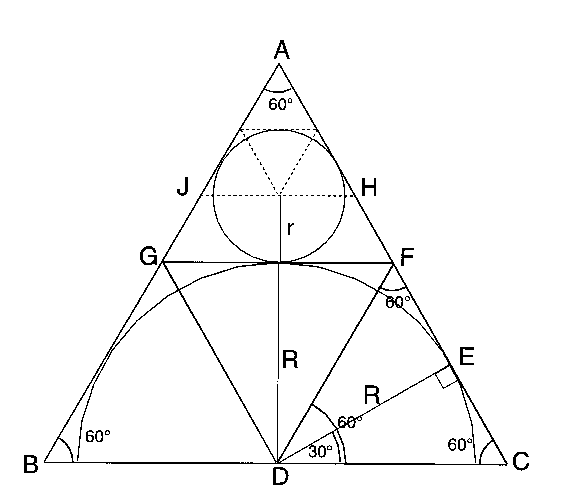
Since a straight line touching the circumference of a circle will unavoidably find itself at right angles to the radius it "touches" - in this case line DE - we know angle DEC to be a right angle. As the whole thing is an equilateral triangle, angle ACB must be 60 degrees. The "missing angle" in triangle ECD (angle CDE) must therefore be 30 degrees.
Triangle ECD can be reflected along line DE to produce the equilateral triangle FCD. Triangle FCD is similar to the whole triangle but with sides half the length, therefore 4 "FCDs'' can fit into ABC in the well known pattern:
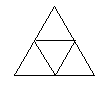
The height of triangle FCD (or any of the other congruent triangles) is R and the height of triangle ABC is twice the height of triangle FCD, that is 2 R .
The upper section of the upper triangle (from the middle of the small circle upwards - AHJ) can be analysed similarly to the semi-circle below, so we find the height of triangle AHJ is 2 r . Therefore the height of triangle AFG = the height of triangle AHJ + r = 3 r . Therefore R = 3 r so the ratio R : r = 3 : 1.
