Squ-areas
Problem
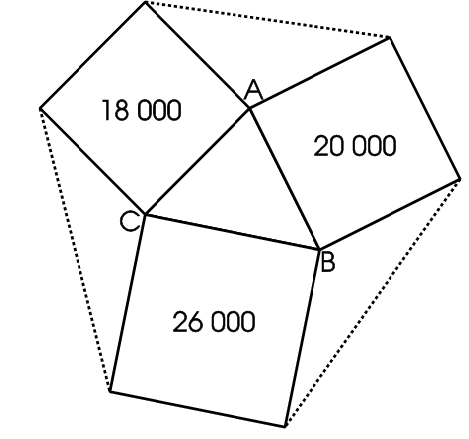
The diagram shows three squares on the sides of a triangle $ABC$.
Their areas are respectively 18 000, 20 000 and 26 000 square centimetres.
If the squares are joined, three more triangular areas are enclosed. What is the area of this convex hexagon?
Student Solutions
Sue, Madras College, arrived at the correct answer using the formula $\frac{1}{2}ab \sin C$. For those not familiar with this formula then do look again at the problem. You may find a more accessible solution if you remember Pythagoras and that:
$26 = 5^2 + 1^2$
$20 = 4^2 + 2^2$
$18 = 3^2 + 3^2$.
This solution was submitted by Sue.
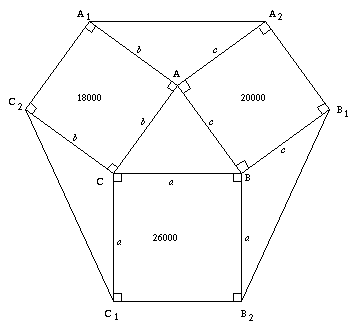
First we change square centimeters into square metres, so $26000$ cm$^2 = 2.6$ m$^2$ , $18000$ cm $^2 = 1.8$ m$^2$ and $20000$ cm$^2 = 2$ m$^2$.
Then we put letters at all points shown on the diagram so the three enclosed triangles are triangle $CC_1C_2$, triangle $BB_1B_2$, and triangle $AA_1A_2$.
Let the length of $AB$ be $c$, length of $AC$ be $b$ and the length of $BC$ be $a$. Because of the squares, $BB_1 = AA_2 = c$, $AA_1 = CC_2 = b$ and $CC_1 = BB_2 = a$.
We know the formula for the area of a triangle $ABC$ is $(1/2)absin C$.
In triangle $CC_1C_2$
| $CC_1 = CB = a$ |
| $CC_2 = AC = b$ |
| $\sin(180^{\circ} - C) = \sin C$ (because of the two right angles) |
so triangle $CC_1C_2$ and triangle $ABC$ are equal in area.
Similarly we can prove triangle $AA_1A_2$ and triangle $BB_1B_2$ are also equal in area to triangle $ABC$. Therefore the four triangles are equal in area and we only need to work out one of these areas.
Using the formula $(1/2)ab \sin C$
Area of triangle $ABC$ = $1/2(\sqrt{2.6})(\sqrt{1.8})\sin{C}$ m$^2$
Using the cosine rule we can work out that
$\eqalign{ \cos{C} &=& \frac{2.6 + 1.8 - 2}{2\sqrt{2.6}\sqrt{1.8}} \\ \; &=& \frac{1.2}{\sqrt{4.68}} \\ \; &=& \frac{2}{\sqrt{13}}}$Therefore we know that
$\eqalign{ \sin{C} &=& \frac{\sqrt{13 - 2^{2}}}{\sqrt{13}} \\ \; &=& \frac{3}{\sqrt{13}}}$Put this in our original equation
$\eqalign{ \mbox{Area of triangle} ABC &=& 1/2(\sqrt{4.68})(\frac{3}{\sqrt{13}}) m^2 \\ \; &=& 1/2(0.6\sqrt{13})(\frac{3}{\sqrt{13}}) m^2 \\ \; &=& 0.9 m^2}$Therefore the area of the hexagon is
| (0.9 m$^2$ \times4) + 2.6 m$^2$ + 1.8 m$^2$+ 2 m$^2$ | = 3.6 m$^2$ + 6.4 m$^2$ |
| = 10 m$^2$ | |
| = 100000 cm$^2$ |
