Bound To Be
Four quadrants are drawn centred at the vertices of a square . Find
the area of the central region bounded by the four arcs.
Age
14 to 16
Challenge level
Problem
Image
|
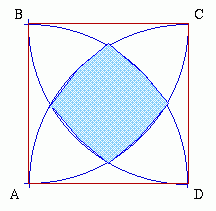
$ABCD$ is a square of side 1 unit.
Arc of circles with centres at $A, B, C, D$ are drawn in.
Prove that the area of the central region bounded by the four arcs is: $(1 + \pi/3 + \sqrt{3})$ square units. |
Student Solutions
This problem attracted several correct answers anonymously submitted by students at Madras College . This solution is included because of its brevity:
Image
|
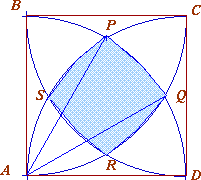
$AD = 1$ unit, which is the radius of the circle centre
$A$.
The coordinates of $P$ are $(AD \cos 60^{\circ} , AD \sin
60^{\circ} ) = ({1\over2}, {\sqrt{3}\over2})$
Similarly coordinates of $Q$ are $(AD \cos 30^{\circ} , AD
\sin 30^{\circ} ) = ( {\sqrt{3}\over2},{1\over2})$ and angle $PAQ$
is $30^{\circ}$.
Area of square $PQRS = ({1\over2} - {\sqrt{3}\over2})^2 +
({\sqrt{3}\over2} - {1\over2})^2 = 2 - \sqrt{3}$
Area of a segment $PQ$ = [${1\over12}$ area of circle, centre
$A$ radius $1$ unit] - [Area of Triangle $APQ$ ]
Using the formula ${1\over12}\pi r^2$ for the $30$ degree
sector and ${1\over2} ab\sin C$ for the area of the triangle we
get:
Area of a segment $PQ = {1\over12} \pi.1.1 -
{1\over2}.1.1.{1\over2} = {\pi\over12} - {1\over4}$ \par Bounded
area = area of square $PQRS$ + area of 4 equal segments
Bounded area $= 2 - \sqrt{3} + 4 ({\pi\over12} - {1\over4}) =
1 + {\pi\over3} - \sqrt{3}$
|