Napoleon's Theorem
Triangle ABC has equilateral triangles drawn on its edges. Points P, Q and R are the centres of the equilateral triangles. What can you prove about the triangle PQR?
Problem
Triangle $ABC$ has equilateral triangles drawn on its edges. Points $P$, $Q$ and $R$ are the centres of the equilateral triangles. You can change triangle $ABC$ below by dragging the vertices and observe what happens to triangle $PQR$.
What can you prove about the triangle $PQR$?
Created with GeoGebra |
NOTES AND BACKGROUND
There are many ways of proving this result. One way you might like to try involves tessellation.
(1) Draw any triangle, with angles $A, B$ and $C$ say.
(2) Draw equilateral triangles $T_1, T_2$ and $T_3$ on the three sides of $\Delta ABC$.
(3) Fit copies of the original triangle and $T_1, T_2$ and $T_3$ into a tessellation pattern so that, at each vertex of the tessellation, the angles are $A, B$ and $C$ and three angles of $60^o$ making an angle sum of $360^o$.
(4) Napoleon's Theorem can be proved by simple geometry using a small part of this pattern without even assuming that this tessellation extends indefinitely in all directions, which is intuitively obvious but requires advanced mathematics to prove it.
Getting Started
You might like to make a tessellation with copies of $\Delta ABC$ and three triangles drawn on the sides of $\Delta ABC$ and prove your conjecture from the tessellation. This uses only elementary geometry. An alternative method is to use the Cosine Rule.
Alternatively you can use vectors or complex numbers.
Student Solutions
Image
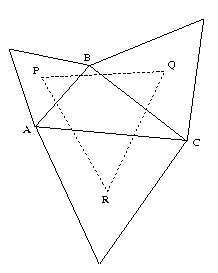
| Triangle $ABC$ has equilateral triangles drawn on its edges. Points $P$, $Q$ and $R$ are the centres of the equilateral triangles. Experimentation with the interactive diagram leads to the conjecture that $PQR$ is an equilateral triangle.
There are many ways to prove this result. Here we have chosen two methods, one which uses only the cosine rule and one which uses complex numbers to represent vectors, and multiplication by complex numbers to rotate the vectors by 60 degrees. |
Another proof using a tessellation of the plane is discussed on the Cut-the-knot website.
First the proof using the Cosine Rule.
The sides of triangle $ABC$ are written as $a, b$ and $c$. Centroids of equilateral triangles are at the intersection of the altitudes so $\angle PAB$ and $\angle RAC$ are both 30 degrees. Hence
$$AP = {2\over 3}.{\sqrt 3 c\over 2}= {c\over \sqrt 3}$$ and $$AR = {2\over 3}.{\sqrt 3 b\over 2}= {b\over \sqrt 3}.$$
It follows that $\angle PAR = (\angle A + 60)$ degrees. By the cosine rule
$$PR^2 = AP^2 + AR^2 - 2AP.AR \cos (\angle A+60) = {1\over 3}(c^2 + b^2 - 2bc \cos (\angle A + 60) \quad (1).$$
Now $ \cos (\angle A + 60) = {1\over 2}\cos A - {\sqrt 3\over 2}\sin A$ and, from $\triangle ABC$: $\cos A = {b^2 + c^2 - a^2 \over 2bc}$ and $\sin A = {2{\rm Area}\triangle ABC\over bc}$. Substituting for $\cos (\angle A + 60)$ in (1) and simplifying the expression gives:
$$ PR^2 = {1\over 3}\left[{a^2 + b^2 + c^2\over 2} + 2\sqrt 3 {\rm Area}\triangle ABC\right].$$
This formula is completely symmetric in $a, b$ and $c$ and it follows that $RQ^2$ and $QP^2$ have the same value and that $\triangle PQR$ is equilateral.
Next the proof using complex numbers as vectors.
We use $\lambda = e^{\pi i/3}$ so that $ \lambda ^2 = \lambda - 1$.
Also multiplying a complex number by $\lambda$ rotates it by 60 degrees.
Referring to the given diagram let $A, B, C$ be represented by the complex numbers $a, b, c$. The third vertex of the equilateral triangle drawn on $AB$ is represented by the complex number $a+ \lambda (b-a)$. Therefore the centre of this triangle P is represented by $p$ where
$$p = {1\over 3}([2 - \lambda ]a +[1 +\lambda ]b).$$ Similarly $$q = {1\over 3}(2 - \lambda ]b +[1 + \lambda ]c),$$
and
$$r = {1\over 3}(2 - \lambda ]c +[1 + \lambda ]a).$$
To show that $PQR$ is equilateral it is sufficient to show that $r - q = \lambda [p - q]$ and this follows using simple algebra and $\lambda ^ 2 = \lambda - 1$.
Teachers' Resources
Why do this problem?
Students can experiment with the interactivity, observe what remains invariant as the inner triangle changes, make a conjecture and then try to prove it.
There are several diffferent ways to prove this result.
One way uses only the Cosine Rule and the area formula for a triangle. It is quite short as it produces a formula that is entirely symmetric in $a, b$ and $c$, the lengths of the sides of the inner triangle, and then uses a symmetry argument to complete the proof. This in itself is a good thing for students to see and be aware of.
An alternative method uses a tessellation with copies of $\Delta ABC$ and three triangles drawn on the sides of $\Delta ABC$. This uses only elementary geometry. There is a second interactivity to aid students in visualising the tessellation and proving the result by this method.
Either of these two methods provide a Stage 4 challenge.
Alternatively you can use vectors or complex numbers (a Stage 5 challenge).
Possible approach
Key questions
