Chord
Equal touching circles have centres on a line. From a point of this
line on a circle, a tangent is drawn to the farthest circle. Find
the lengths of chords where the line cuts the other circles.
Problem
Three circles all of radius 2 cm touch as shown in the diagram.
Image
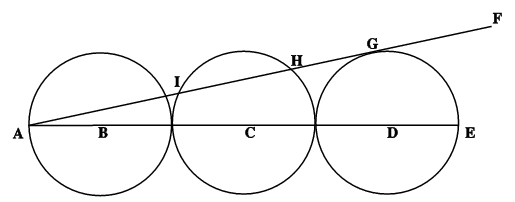
A straight line $AG$ is tangential to the third circle, meeting the middle circle at $H$ and $I$.
How long is $HI$?
What if there are four or more circles?
Getting Started
Similar triangles.
Student Solutions
Image
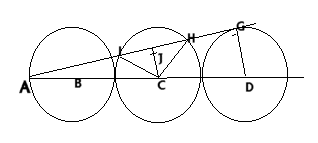
|
Congratulations to four students from
Madras College, Gordon and Alan from S6, Sue Liu from S4 and David
from S3. They all sent excellent solutions to this problem
including complete proofs of the general case. Answers also arrived
from St Peter's College in Adelaide,
Australia.
This is David's proof of the first part: Lines $CH$ and $CI$
can be drawn in. Both have length $R$ or 2 cm.
|
$ICH$ is an isosceles triangle which can be split into two congruent right angled triangles by drawing line $CJ$, where $J$ is the midpoint of chord $IH$.
Triangle $AJC$ is similar to triangle $AGD$, with a ratio of 6 cm to 10 cm or 3:5.
Line $GD = R= $2 cm,
Line $CJ =$ 3/5 $GD= $1.2 cm.
Image
|
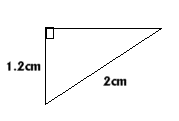
Both right angled triangles $CJH$ and $CJI$ have lengths as
below and the length $JH$ can be worked out using Pythagoras'
theorem.
$JH^2 = 2^2 - 1.2^2 = 4 - 1.44 = 2.56 = 1.6^2$ So $JH = $1.6 cm and the chord $JH = $2(1.6)= 3.2 cm. |
This is Gordon's proof of the general case of n circles where $AG$ cuts the m th circle at $I$ and $H$.
Image
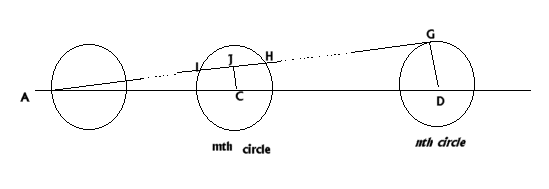
$\angle ACJ$ is similar to $\angle ADG$
$\Rightarrow AD = 2 \times2(n - 1) + 2 = 4n - 2$ units
$\Rightarrow AC = 4m - 2$ units.
$\eqalign{ \frac{JC}{AC} &= \frac{DG}{AD} \\ \frac{JC}{4m
- 2} &= \frac{2}{4n - 2} \\ JC &= \frac{4m - 2}{2n -
1}}$
$\angle IHC$ is isosceles and $\angle CJI = \angle CJH =
90^{\circ}$.
Hence, by Pythagoras' theorem, $$IH = 2JH = 2\sqrt{2^2 -
\left(\frac{4m - 2}{2n - 1}\right)^2}$$ Simplifying this expression
gives $$IH = \frac{8}{2n - 1}\sqrt{n(n - 1) - m(m - 1)}$$ Checking
this where $n=3$ and $m=2$ $$IH = \frac{8}{5}\sqrt{6 - 2} =
\frac{16}{5} = 3.2$$
Teachers' Resources
Why do this problem?
The problem calls for simple geometrical reasoning (nothing more complicated than similar triangles) and leads to an obvious generalisation. Finding the solution is the beginning of the next stage:how can I explain my method?
is this the best method?
what if...can I generalise this result?
Key questions
What do you know about the tangent to a circle and its radius?What do you know about the perpendicular from the centre of a circle to a chord?
Can you spot any similar triangles?
If two sides of a right-angled triangle are in the ratio 3:5 what can we say about the third side?
