Golden ratio
Solve an equation involving the Golden Ratio phi where the unknown
occurs as a power of phi.
Problem
The 'divina proporzione' or golden ratio, represented by the Greek letter phi, is derived from the equation below where $a$ and $b$ are parts of a line.
Image
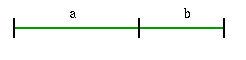
|
$a+b:a=a:b$
i.e. $ \frac{a+b}{a}=\frac{a}{b}=\Phi\ \quad $(phi)
|
If $b = 1$ show that
$\Phi = a = (\sqrt 5 + 1 )/2 = 1.618034...$.
In the following equation
what does $x$ equal?
$$\Phi^{\left(\Phi^x-\frac{x-1}{\Phi}\right)}-\frac{1}{\Phi}=x$$
Getting Started
Take $b = 1$ and write the equation in terms of $a$. Then solve this equation to find the golden ratio.
Student Solutions
One solution is $x = 2$.
Can you discover whether this is the only solution and justify your claim?
Teachers' Resources
Why do this problem?
This problem introduces the Golden Ratio as the solution of a quadratic equation and links to many other investigations. A solution to the equation can be found by trial and error.Possible approach?
To motivate the topic why not introduce several problems where the students can discover that the Golden Ratio occurs in very different contexts and reinforce their own understanding of the algebra that occurs. For example:Golden Powers , Golden Triangle and Golden Eggs.
