Corridors
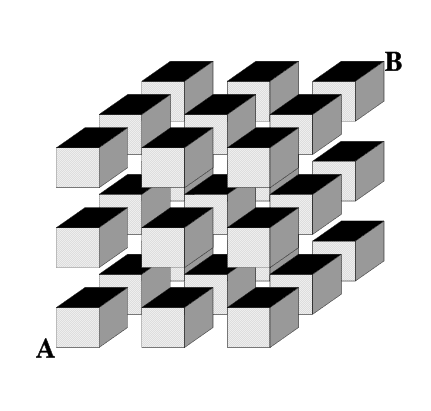
A 10x10x10 cube is made from 27 2x2 cubes with corridors between
them. Find the shortest route from one corner to the opposite
corner.
Problem
9 identical squares of side 2 units are separated by empty strips also of 2 units width.
What is the shortest route from A to B, assuming you can only go around the edges of the squares?
Image
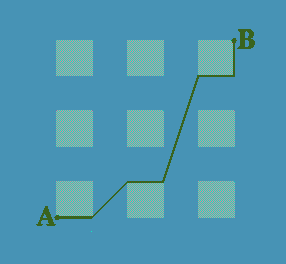
Now, consider 27 identical cubes of side 2 units which are separated by corridors also of 2 units width. What is the shortest distance from A to B?
Image
Student Solutions
In essence this problem is about Pythagoras' Theorem and optimising the shortest route which takes you `to the right, upwards and backwards' to best effect.
Luke from Flegg High approached this problem using vectors and was able to build on his earlier work with the 2D part of the problem. He used three dimensional co-ordinates and his solution of $4 + \sqrt{100 + 64 + 64}$ was readily agreed upon until the shown solution was arrived at. But thank you Luke, your insight into the problem allowed others at the site to find an alternative and sadly for you, a shorter route.
First, for the 2D case, we use coordinates in the obvious way with $A(0,0)$ and $B(10,10)$. The straight line $y = x - 2$, from $(2,0)$ to $(10,8)$, provides a way through, just glancing the corners of the cubes it passes, giving the shortest route to be $4 + 8\sqrt{2}$.
The 3D problem extends the ideas used in the 2D case. We assign coordinates again, with $A(0,0,0)$ and $B(10,10,10)$. Imagine looking vertically down on the stack of 27 cubes, you will see 9 squares (the tops of the top layer of cubes) and a corridor in a vertical plane by analogy with the plane case. This vertical plane, containing $(2,0,0)$ $(2,0,2)$ $(2,0,10)$ and $(10,8,0)$ $(10, 8,8)$ $(10,8,10)$ etc., provides a corridor.
IMAGINE TAKING A PIECE OF PAPER of height 10 units, placing it vertically, threading it through the corridor and wrapping it around the outside so that it has one corner at $A$ and the diagonally opposite corner at $B$. This piece of paper has dimensions $(4 + 8\sqrt{2})$ units by 10 units. One route is from $A(0,0,0)$ to $(2,0,2)$ to $(10,8,8)$ to $(10,10,10)$ but there is a shorter route which goes through a point on the edge just below $(2,0,2)$.
If you flatten the paper out and mark the diagonal this gives the length of the route from A to B on this piece of paper which is $\sqrt{244 + 64\sqrt{2}}$ giving the approximate value 18.29 units (to 2 decimal places).
