Counters
Problem
To play this game, you'll need a friend and twelve counters.
The aim of the game is to be the player who takes the last counter or counters.
How to play:
Lay out the counters in an array like this:

The first player chooses a counter and removes it from the array, and also removes all the counters that touch it.
The second player also chooses a counter and removes it from the array, and also removes all the counters that touch it.
Play continues like this with players taking it in turns, until one of the players removes the last counter (or counters). That player is the winner!
Here is an example, where the first player has chosen the counter with the black cross. This means that all the counters coloured red in the picture below are removed:
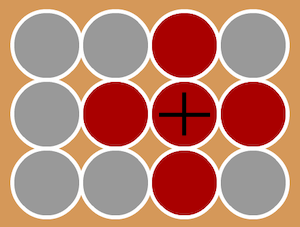
So, now the counters left look like this:

Player two then decides to choose the bottom left counter, so all the counters coloured blue in the picture below are removed:

So now there are just these counters left:
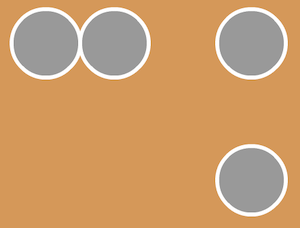
Player one then chooses the top left counter, and removes it with the one that is touching it:

Player two now decides to choose the bottom right counter and removes it:

So player two takes the last counter and is the winner!
Play the game a few times with a friend.
Now begin to think about your strategy, in other words, how you can make sure you win.
If the first player takes the middle counter from the first column on the left, how could the second player make sure he or she wins?
If the first player removes the middle counter in the second column to start with, what should the second player do to win the game?
Do you think it is better to be the first player or the second player? Why? Try to explain your reasoning by giving some examples.
Getting Started
Once player 1 has had their first turn, what options are there for the second player? Which counter/s could they take? How will you know which would be the best to remove?
Might it help to record the results of the games?
How many different ways are there for the first player to begin? Does the grid have any symmetry that may help you?
Student Solutions
Ryan and Adam from Moorfield Junior School have obviously spent some time looking at this game. They have chosen two situations which they have broken down step by step:
Ryan and Adam concluded that it is better to be player two because you can take control of the game and win.If player one takes the middle counter out of the first column then player two should take all the counters from the fourth column (by taking the middle counter in the fourth column). Then there are two choices. Player one will pick one of the choices then player two will pick the other choice and player two wins.
If player one takes the middle counter in the second column then player two will take all the counters from the fourth column (by selecting the middle counter in the fourth column). Then there are four choices. Player one takes one of the choices, then player two takes another of the choices, then player one takes another of the choices and then there is one choice left. Player two takes the last counter and wins.
Do you agree? What other possible moves could player one start with? Would these be as good for player two? If you investigate this game further, email us your findings.
Teachers' Resources
Why do this problem?
Children will be motivated to work systematically as they play this game because they will want to think ahead.
Key questions
Would it be a good idea to start with a smaller number of counters. How about four arranged in a square?
How many different ways are there for the first player to begin?
Does the grid have any symmetry that may help you?
Possible extension
Learners could try with a larger number of counters, or the counters arranged differently.
Possible support
Working with 2cm squared paper and counters will mean that children can simplify the game easily.
