A Square Deal
Problem
Complete the magic square using the numbers $1$ to $25$ once
each.
Each row, column and diagonal adds up to $65$.
Each square is identified by its column and row:
Here are the clues:
Perfect squares are in b5, b3, d3, b1 and c1.
Prime numbers are in a5, c5, e5, c4, a3, c3, e3, e2 and a1.
Triangular numbers are in d5, e4, d3, a1, e1 and c2.
Perfect cubes are in d3 and b2.
Powers of 2 are in b5, b2, e2 and b1.
Palindromic numbers are in a5 and d1.
Factors of 100 are in b5, d5, c4, b3, d3, a2 and e2.
The median of all the numbers is in c3.
Row 3 and column c are all odd.
Numbers that are the same upside-down are in a5, d3 and b2.
This problem is taken from the summer 2003 edition of "Mathematical Pie", a booklet of mathematical challenges published three times a year by The Mathematical Association. For more details about how to subscribe, see the MA website or phone 0116 221 0013.
Getting Started
Make a list of all the numbers that could satisfy each clue i.e.
a list of all the perfect squares, another of all the prime numbers
etc. It might be a good idea to list underneath the possible
squares that these numbers go in.
Write the numbers from $1$ to $25$ and cross them out as you fit
them in the magic square.
How could you work out the median?
How about looking for squares that are listed in more that one clue
to get you started?
Keep crossing off numbers and squares from your lists as soon as
you've placed them in the magic square - you'll soon notice that
some answers will just fall out!
Student Solutions
Thank you to everyone who sent in correct answers to our magic square problem. As usual, here we will give some examples of those of you who gave us great explanations as to how you approached it.
Gitty and Gabriel from Bournemouth Jewish Day School wrote an extremely clear account:
We wrote down the square numbers, prime numbers, triangle numbers, cube numbers, powers of two, palindromic numbers, factors of $100$, upside down numbers and the median. All our answers had to be $25$ or less.
We drew a $5$ x $5$ grid and put in the median as $13$ in c3.
Next we found a5 because it is palindromic, prime and upside down, $11$.
Then we found d1 because it is palindromic, $22$.
After that we found a1 because it is the only prime and triangular number, $3$.
Next was d3 because it is square, triangular, cube, upside down and a factor of $100$, $1$.
Now b2 must be $8$ because it is the only cube left. It is also upside down and a power of two.
Then e5 as it is only said to be prime, $23$.
As there is only one space left in the diagonal a1 to e5, we have $47$ so d4 must be $65 - 47 = 18$. $18$ is not found in any group.
e4 came next as 6 - triangular.
Then we found e2 because it is prime and a factor of $100$ i.e. $2$.
a2 is a factor of $100$ that is not in any other group, $20$.
a3 is a prime number and nothing else, $7$.
c4 is prime and a factor of $100$, $5$.
We can now find column a because only a4 is missing. $65 - 41 = 24$.
Now we can find row 4, $65 - 53 = 12$ (b4).
We then spotted a pattern on the diagonal a5 to e1. We discovered that it was $11, 12, 13$ so we tried $14$ and $15$ and we checked and found that e1 has to be triangular and so can be $15$ and then d2 can be $14$. Also $11 + 12 + 13 + 14 + 15 = 65$.
We can now find c2 to complete row 2, $65 - 44 = 21$ and it is also triangular.
d5 is $10$ because $65 - 55 = 10$ and $10$ is also triangular.
Next e3 is $19$ because $65 - 46 = 19$ and e3 is also odd and prime.
Next b3 is $25$ because $65 - 40 = 25$ and $25$ is square and a factor of $100$.
Only b1, c1, b5 and c5 are left. c5 is not square so it must be $17$ as it is prime.
This means that c1 must be $65 - 56 = 9$ and $9$ is odd and square .
b5 is square and a factor of $100, 4$.
So b1 is $16$, square and a power of $2$.
We checked by adding all the rows and columns and they made $65$ each.This is what the square looks like:
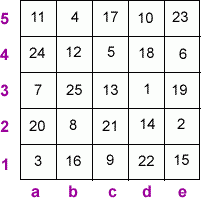
Bronya from Tattingstone School used a very systematic approach too, although slightly different from Gitty and Gabriel's:
I know straight away that c3 = $13$ because $13$ is the median of all the numbers.
I also know that d3 had to be $1$ as it had to be odd, it was a factor of $100$ and it looked the same upside-down. The numbers that looked the same upside-down were $1, 8 and 11$. I know it couldn't be $8$ as $8$ is even. It couldn't be $11$ either as $11$ isn't a factor of $100$.
I also worked out that a5 = $11$ because it was a prime number, it was a palindromic number and it was a number that looked the same upside-down.
This told me that d3 = $8$ as it was the only number left that looked the same upside-down.
Also it meant that d1 = $22$ because $22$ is the only other palindromic number left.
I worked out that b3 = $25$ because b3 was odd, it was a perfect square and it was a factor of $100$. The perfect squares left were $4, 9, 16 and 25$ but only $25$ was a factor of $100$.
I know that c4 = 5 because it was a factor of $100$ and it was a prime number which left me with $2$ or $5$ as I had already used $25$. I also know that it had to be odd.
That meant that e2 = $2$ because like c4, the number was a prime and a factor of $100$ but as a definite answer e2 was also a power of $2$.
I carried on like this until I had filled in the whole square.
I listed the numbers that fitted with the fact:Perfect Squares: $1, 4, 9, 16, 25$
Prime Numbers: $2, 3, 5, 7, 11, 13, 17, 19, 23$
Triangular Numbers: $1, 3, 6, 10, 15, 21$
Perfect Cubes: $1, 8$
Powers of $2$: $2, 4, 8, 16$
Palindromic Numbers: $11, 22$
Factors of $100$: $1, 2, 4, 5, 10, 20, 25$
Median: $13$
Numbers that are the same upside-down: $1, 8, 11$
This is a very good strategy, writing down a list like this. Gemma from Hillside Community Primary School also did this in order to help her get the solution.
Katelyn from Kilvington Girls Grammar in Australia wrote to us with some handy hints for how to start:
Rule up a graph $25$ x $10$
In the $10$ vertical lines write an abbreviation for the attributes required.
In the $25$ horizontal lines write the numbers $1 - 25$.
Tick what attributes each number has.
Rule up an identical $5$ x $5$ grid, shown in the problem.
From the clues given, write what attributes each square requires.
Transfer the numbers with all of the required attributes into the appropriate square. This will reduce the number of possibilities per square.
Fill in the squares with only one possible answer. Then eliminate these numbers from other squares.
When you have at least $3$ numbers in a line, add these numbers together and subtract the total from $65$.
Now select the appropriate numbers from the selection in each square tocomplete the row.
Continue crossing out the numbers as you select them. This will reduce thepossible selection in other squares.
Well done also to Claire from St Ives, Haslemere, Duncan from Balgowan Primary School, Samuel from Bispham Drive Junior School, Stefan from Sacred Heart Roman Catholic Primary School and Suzy who was working from home, who all got the correct answer.
