Symmetry Challenge
How many symmetric designs can you make on this grid? Can you find them all?
Problem
Symmetry Challenge printable sheet
In this activity, we are going to shade the squares of this grid with one colour to make different designs.
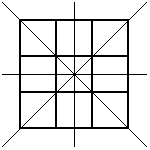
There are a few rules that our designs need to follow:
- Whole squares have to be shaded, rather than parts of squares.
- Each design must have at least one line of symmetry.
- Each new design you come up with must be different from all of the others. If two designs would look the same if you rotated or reflected them, they do not count as different designs in this task.
Have a go at making some designs. How many can you find? You might like to shade your designs on squared paper or on this sheet of blank grids.
If you wanted to find every possible design, how would you do this?
Getting Started
The 3 by 3 grid has 4 lines of symmetry. How might this help?
Try shading only one square. What symmetries are possible?
Try shading 2, 3, 4, ... squares. What symmetries are now possible?
How helpful would this table be?
| Lines of symmetry | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||||
| Shaded squares | 1 | |||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
What other rows or columns could you add to this table?
Student Solutions
Christina from Marborough Primary, London has given this one some thought and made the sensible suggestion of trying to find all the symmetrical patterns with one coloured square, then with two squares, then three, then four. That's just what Tom has done below.
Tom was very careful in trying to make sure that he found them all. First, he looked for patterns with no coloured squares. Of course, there's only one of those:
Then he looked for patterns with one coloured square. Here are the patterns he found:
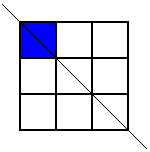
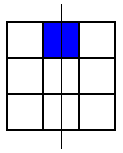
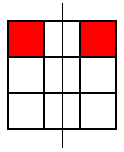
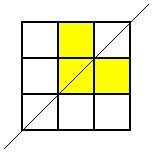
but that was the only one. Then he looked for patterns with this square coloured where the line of symmetry was horizontal, but he came up with the same one again (rotated, of course). Then he looked for ones where the line of symmetry was diagonal. Here are the two patterns he found:
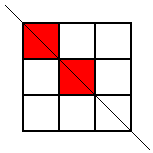
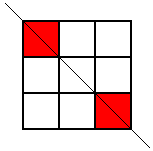
These were the only symmetrical patterns with a corner square shaded. Next he shaded the top centre square and looked for patterns with a vertical line of symmetry. Here's what he found:
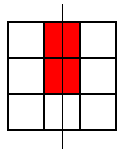
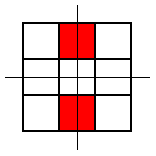
He noticed that he wouldn't get any new patterns by looking for ones with horizontal lines of symmetry, so he looked for patterns with a diagonal line of symmetry. This is the only one he found:
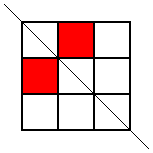



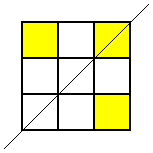
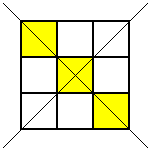
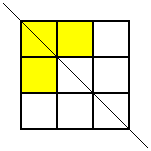
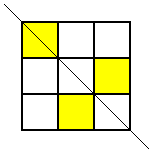

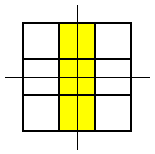
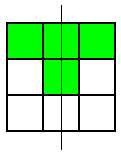

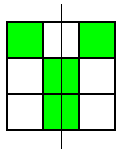
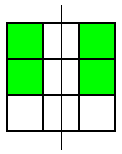
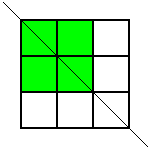
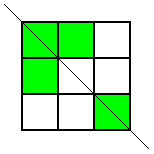
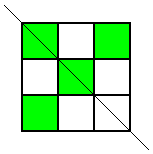
Thank you for your all your ideas everyone.
Teachers' Resources
Why do this problem?
The problem requires learners to recognise and visualise the transformation of a 2D shape, and invites them to work systematically in a spatial environment. It is a problem that is accessible to most pupils even if they need support in organising and presenting their ideas and ensuring the completeness of their solution.
Possible approach
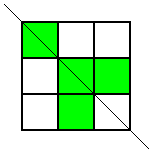
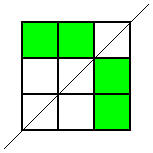
You could start by displaying these two shaded grids on the board to simulate a discussion about reflection symmetry. It might also help to have some blank $3$ by $3$ grids on the board for learners to shade as they talk.
- Are the patterns you have all symmetrical?
- Which are the same and which are different?
- Are there any more with the same number of squares shaded?
Key questions
Possible extension
The problem can be extended to discuss larger square lattices, e.g. $4$ by $4$ and whether there are any differences between even and odd lengths of side. The activity Shady Symmetry is also an extension possibility.
