You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?
Age 5 to 7
Challenge Level
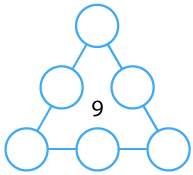
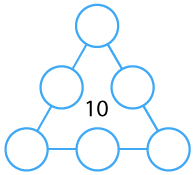
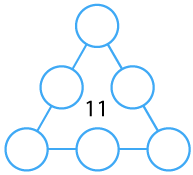
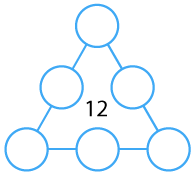
Arrange the numbers 1 to 6 in each set of circles below.
The sum of each side of the triangle should equal the number in the centre of the triangular shape.
How are you going about trying to find an arrangement that works?
You might like to use this interactivity to try out your ideas.
You can drag the numbers into the circles, and, if you like, you can put the total in the centre of the circle to remind you what you are aiming for!
You may find this sheet of blank triangles useful for recording your ideas.
Once you've had a chance to think about it, click below to see how three different pupils began working on the task.
Dan said:
"I used counters which had 1 to 6 on them.
I put the counters in a triangle in any old way, then I added up the sides.
Then I moved the counters around to try and get the right total on each side."
Emma said:
"I noticed that three of the numbers are odd (1, 3 and 5) and three of the numbers are even (2, 4 and 6). I thought this might help.
I know that 9 is an odd number so it can be made using odd + odd + odd or using even + even + odd."
Farah said:
"If I want a small total on each side, I'll need small numbers in the corners of the triangle."
Can you take each of these starting ideas and develop it into a solution?
This activity originally featured in the hands-on Brain Buster Maths Boxes, developed by members of the NRICH Team and produced by BEAM. These resources are out of print but can still be found on Amazon.
NRICH is part of the family of activities in the Millennium Mathematics Project.