Transforming the letters
Problem
In Miss Chan's class, a group were working with a box of large
wooden capital letters. They were exploring what happened when they
rotated them one half turn, or flipped them sideways and from top
to bottom.
They started with "F". They found four Fs in the box.
"Billy, you just push yours into the middle of the table," said
Katie who was rather bossy, "then we can see how the others
change."
Here is Billy's F:

"I'll turn my F upside-down," continued Katie,
"that's half a turn."
"A $180^o$ turn about its centre," remarked Ali.
This is what Katie's looked like:

George said, "I'll flip mine over sideways."
Here is George's F:

"That leaves me to flip my F from top to bottom,"
said Ali.
So then Ali's looked like this:

"Look, they are all different. I wonder if all the
letters are like that. Which ones shall we try?"
Katie had spelt out Miss Chan's name with four of the letters:

"Let's try with those," suggested George. So they did.
What did they find out?
"What happens if you do a half turn followed by a sideways flip?" wondered Ali. "Do you think any of the letters in the box get back to the same as they were to begin with?"

They did find some which did just that. Which letters are they?
Do these letters also go back to the same if you do a half turn followed by a flip from top to bottom?
Getting Started
Student Solutions
Sapna who goes to Sacred Heart School, looked at what happens to the letters of the alphabet when they are turned through a half turn, followed by a sideways flip. She drew out the letters one at a time and here are the ones that stay the same:
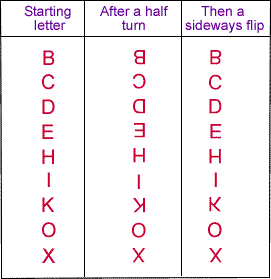
Of course, it will depend slightly on how you write the letters, but well done Sapna! Sam from Bispham Drive Junior School agreed with this list and explains:
These letters all worked because they have a horizontal line of symmetry. When doing a half turn they are upside down and backwards and flipping them over makes them right.
Can anyone answer the rest of the question? Do these letters stay the same with a half turn followed by a flip from top to bottom?
