Terminology
Given an equilateral triangle inside an isosceles triangle, can you find a relationship between the angles?
Problem
Terminology printable worksheet
The green triangle is an isosceles triangle while the blue triangle is an equilateral triangle.
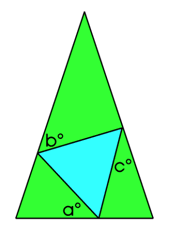
Find $a$ in terms of $b$ and $c$.
What can you say about the triangles if $a = b = c$?
Getting Started
What do you know about the angles in an equilateral triangle?
What do you know about the angles that meet on a straight line?
What do you know about the angles in an isosceles triangle?
Start by filling in the diagram with the information you know.
Student Solutions
Correct solutions from Mary of Birchwood High School and Andrei of School 205 Bucharest have contributed to the edited solution below.
As triangle DEF is equilateral, all its angles are $60$ .
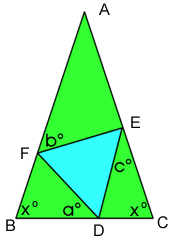
Angle AEF $= 180 - 60 - c = 120 - c$
Similarly
Angle BFD $= 120 - b$
Angle EDC $= 120 - a$
From triangle FAE, I calculate angle A:
As triangle ABC is an isosceles Angle ABC $=$ Angle ACB $= x$
Therefore $180 - (120 - b + a ) = 180 - (120 - a + c )$
Therefore $60 + b - a = 60 + a - c$
Therefore $2a = b + c$
Therefore $a = (b + c)/2$
Part Two
If $a=b=c$
Angle ABC $= 180 - (120 - b + a ) = 180 - (120 - a + a ) = 60$
Angle ACB $= 180 - (120 - a + c ) = 180 - (120 - a + a ) = 60$
Therefore angle BAC is $60$
Therefore triangle ABC is equilateral.
Teachers' Resources
This printable worksheet may be useful: Terminology.
This problem requires students to know the properties of equilateral and isosceles triangles.
