Sept 03
What is the last digit of the number 1 / 5^903 ?
Problem
What is the last digit of the number
Image
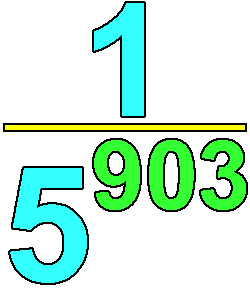
Getting Started
Another way of writing 1/5 !
Now look at first few powers and see what happens.
Student Solutions
Some nice solutions. Well done. The ones from Andrei of School 205 Bucharest and Sana, Jenny, Chris and Rosion of Madras College, St. Andrews are given below. Correct solutions were also recieved from Jonathan and Philip and Michael (all from Madras college as well as Mary of Birchwood High School.
$$\frac{1}{5^{903}} = \frac{1}{5^{903}} \cdot 10^{903} \cdot 10^{-903} = 2^{903} \cdot 10^{-903}$$ As $10^{-903}$ only establishes where the decimal point is placed, to calculate the last digit of the number I must find the last digit of $2^{903}$.
The last digits of the power of 2 are:
\begin{array} \textrm{}& \textbf{Number}
& \textbf{Last Digit} \\&2^1 & 2 \\&2^2 & 4
\\&2^3 & 8\\ &2^4 & 6 \\&2^5 & 2 \\
&\dots & \; \\ &\dots & \; \\ &\dots & \;
\\ &\dots & \; \\ &2^{(4k+1)} & 2 \\
&2^{(4k+2)} & 4 \\ &2^{(4k+3)} & 8 \\
&2^{(4k+4)} = 2^{4(k+1)} & 2 \\ \end{array}
Now, all I have to do is to find in what category $2^{903}$ is.
But $903 = 4 x 225 + 3$ (i.e $k = 225$) So, the last digit of the number is 8, and the last digit of $1/(5^{903})$ is also 8.
OR
The last digit of the number $1/(5^{903})$ is 8.
First of all we made a table to see if there is a pattern or relationship between the powers of 5 and the last digit of the answer to this sum:
\begin{array} \textrm{} & \textbf{n} &
\mathbf{1/5^{n}}& \textbf{As a decimal} & \textbf{Last
digit} \\& 1 & 1/5 & 0.2 & 2 \\& 2 & 1/5^2
& 0.04 & 4 \\& 3 & 1/5^3 & 0.008 & 8
\\& 4 & 1/5^4 & 0.0016 & 6 \\& 5 & 1/5^5
& 0.00032 & 2 \\& 6 & 1/5^6 & 0.000064 & 4
\\& 7 & 1/5^7 & 0.0000128 & 8 \\& 8 & 1/5^8
& 0.00000256 & 6 \\& 9 & 1/5^9 & 0.000000512
& 2 \\& 10 & 1/5^{10} &0.0000001024 & 4
\\\end{array}
The last digit will be either 2, 4, 6 or 8.
The last digit in pattern 1 is 2. The last digit in pattern 5 is also 2. The last digit in pattern 9 is again 2. The difference between the pattern numbers is 4.
Also this is the same for pattern 2, pattern 6 and pattern 10, which all have the last digit 4.
$6 - 2 = 4$
$10 - 6 = 4$
This is the same for pattern 3 and 7, last digit 8.$7 - 3 = 4$
Again for pattern 4 and 8, last digit 6.
$8 - 4 = 4$
So if you know $n$ (pattern number) you just have to take away 4 as many times till you reach a number from 1 and 10, as you know the last digits of those numbers.
$n = 903$
$903 - (4 x 225) = 903 - 900 = 3$
So then you look at the table and find out what the last digit of pattern 3 is.
The last digit of pattern 3 is 8.
