Circumnavigation
Problem

The sides of a triangle are 25, 39 and 40 units of length.
Find the diameter of the circumscribed circle.
Getting Started
No difficult calculations are necessary
Pythagorean triples could be useful
And some circle theorems
Student Solutions
Solutions were received from Mary from Birchwood High School; Sana, Jenny, Chris and Rosion of Madras College, St. Andrews; as well as Andrei from School 205 Bucharest.
Some hard work went into these solutions but a little more reflection at the start of the problem could have made it much easier and reduced the consequent errors that appeared.

The first thing to look for and notice is Pythagorean triples "hidden" in the sides.
Triangle ABC has AB = 25, AC = 40 and BC=39.
Draw a line from A to BC meeting BC at P so that it divides BC into two parts of lengths BP=7 and PC=32.
AP is perpendicular to BC and AP = 24 (Pythagoras' theorem).
N.B. In triangle APB, $AP^2 = AB^2 - PB^2$
In triangle APC, $AP^2 = AC^2 - PC^2$
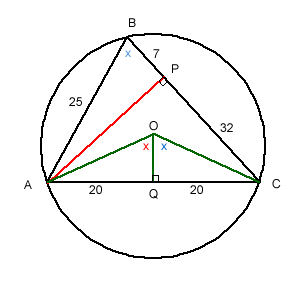
Let angle AOQ = x °.
Therefore angle COQ is x (by symmetry)
Angle ABC = 1/2 Angle AOC = x (angle at centre and circumference)
The radius of the circle is OA.
In triangle AOQ
AO = 20/sin x
In triangle ABP
sin x = 24/25
Therefore OA = (20 x 25)/24 = 125/6
Therefore the diameter is 125/3 units (exactly)
