Ruler
The interval 0 - 1 is marked into halves, quarters, eighths ...
etc. Vertical lines are drawn at these points, heights depending on
positions. What happens as this process goes on indefinitely?
Problem
On the interval 0 to 1 vertical lines are drawn at the points
$x={k\over 2^n}$ where $k$ is an odd positive integer. The height
of the lines at 0 and 1 are 1 unit, the height of the line at
$x={1\over 2}$ is ${1\over 2}$ unit, the height of the line at
$x={1\over 4}$ and $x={3\over 4}$ is ${1\over 4}$ unit and the
height of the line at ${k\over 2^n}$ is ${1\over 2^n}$ for all
values of $k$.
Now consider the line $y=h$ where ${1\over 2^n} > h > {1\over 2^{n+1}}$ . How many of the vertical lines from $x=0$ to $x=1$ does it cut?
What happens to the heights of these lines as $n$ gets larger? What happens to the number of lines cut as $n$ gets larger?
Now consider the line $y=h$ where ${1\over 2^n} > h > {1\over 2^{n+1}}$ . How many of the vertical lines from $x=0$ to $x=1$ does it cut?
What happens to the heights of these lines as $n$ gets larger? What happens to the number of lines cut as $n$ gets larger?
Getting Started
Apart from the very start of the process, the number of lines cut
for each subsequent set of vertical spikes is doubled so giving a
geometric sequence.
Student Solutions
Andaleeb sent in this excellent solution.
The diagram shows some of the vertical lines drawn for values of x between 0 and 1 as described in the question. The lines are of height 1 unit at x = 0 and 1, of height ${1\over 2}$ units at $x= {1\over 2}$ , of height ${1\over 4}$ units at $x= {k\over 4}$ and ${1\over 8}$ units at $x= {k\over 8}$ and so on... up to ${1\over 2^5}$ at ${k\over 2^5}$ where $k$ is a positive integer.
| n | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $\dots$ | $n$ | $n+1$ |
| Height | $1$ | ${1\over 2}$ | ${1\over 4 }$ | ${1\over 8}$ | ${1\over 16}$ | ${1\over 32 }$ | ${1\over 64}$ | $\dots$ | ${1\over 2^n}$ | ${1\over 2^{n+1`}}$ |
| Lines cut | $2$ | $1$ | $2$ | $4$ | $8$ | $16$ | $32$ |
$\dots$
|
$2^{n-1}$ | $ 2^n$ |
Image
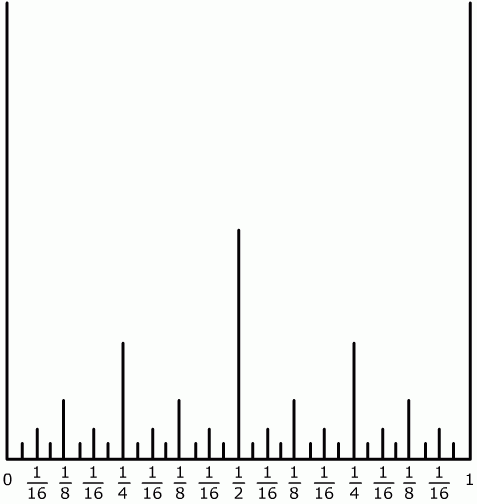
Thus if the height $h$ lies in ${1\over 2^n} > h> {1\over 2^{n+1}}$ then the number of lines cut is given by $$ 2 + 1 + 2 + 4 + 8 + ... + 2^{n-1} = 2 + {{2^n - 1} \over {2 - 1}} = 2^n + 1.$$ As $n$ tends to infinity the height of the lines tends to 0 and the number of lines cut tends to infinity.
