Complex Rotations

Well done Christopher Tynan, St. Bees School, for this very nice solution and also Andrei Lazanu, School No. 205, Bucharest, Romania and Jesse Rasowsky of Bethlehem Central High School and Matthew Hartley.

Below the complex numbers $3-i$ and $2-10i$ are plotted, as well as their corresponding image when multiplied by -1.

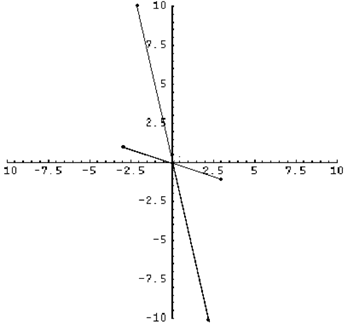
Our conjecture is that multiplying a point on the Argand diagram by -1 is equivalent to a 180 degree rotation about the origin.

Let $(a,b)$ on the Argand diagram represent the complex number $a+ib$, where $i$ is the square root of -1. So, multiplying $a+ib$ by -1, we get $-a-ib$, which is represented by the point $(-a,-b)$ in the Argand diagram. However, the point $(-a,-b)$ is a rotation of the point $(a,b)$ by 180 degrees about the origin. QED.

Using the same numbers for the second part, our conjecture here is that multiplying a complex number by $i$ gives a rotation of 90 degrees anti-clockwise on the Argand diagram.

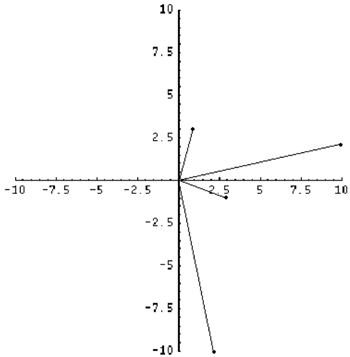
Again, assuming $(a,b)$ is a complex number plotted on the Argand diagram, by multiplying $a+ib$ by $i$, we get the complex number $-b+ai$, which is represented by the point $(-b,a)$ on the Argand diagram. This is equivalent to a rotation of 90 degrees anti-clockwise about the origin. QED.

Assuming we were to multiply the number by $i$ twice, this would give a rotation of 180 degrees (as shown in the first part because $i^2=-1$). Multiplying by $i$ thrice would be equivalent to a rotation of 270 degrees anti-clockwise, or 90 degrees clockwise and four time maps the number onto itself (essentially multiplying by 1). Multiplying by $i$ $n$ times is equivalent to rotating the point 90 degrees anti-clockwise $n$ times. Therefore; if $n$ is 0 mod 4, it has no effect; if $n$ is 1 mod 4, it's equivalent to an anti-clockwise rotation of 90 degrees; if $n$ is 2 mod 4, it's equivalent to a rotation of 180 degrees; if $n$ is 3 mod 4, it's equivalent to a rotation of 90 degrees clockwise.

NB. All these rotations are rotations of the initial point (a,b) about the origin as the centre of rotation.