Complex rotations
Choose some complex numbers and mark them by points on a graph.
Multiply your numbers by i once, twice, three times, four times,
..., n times? What happens?
Problem
Image
If you have solved quadratic equations you have met complex numbers. For example if you solve the equation $$x^2-4x+13=0$$ you get the solutions $x=2\pm\sqrt{-9}=2\pm3i$ where $i=\sqrt{-1}$.
The complex number $a+ib$ is represented in the plane by the point with coordinates $(a,b)$. This is called an Argand diagram. Make your own choice of some complex numbers, and mark them on a graph with lines joining the points to the origin. Now multiply your numbers by $-1$ and join their images to the origin. Make and prove a conjecture about the geometric effect of multiplying complex numbers by $-1$.
Again make a choice of some complex numbers and multiply each one by $i$. Draw the complex numbers and their images on a graph and make and prove a conjecture about the effect of multiplying complex numbers by $i$.
What happens if you multiply a complex number by $i$ twice, three times, four times, ..., $n$ times?
Getting Started
The algebra of complex numbers is just like the algebra of real numbers and the only extra information you need to use is that $i^2=-1$.
Student Solutions
Well done Christopher Tynan, St. Bees School, for this very nice
solution and also Andrei Lazanu, School No. 205, Bucharest, Romania
and Jesse Rasowsky of Bethlehem Central High School and Matthew
Hartley.
Below the complex numbers $3-i$ and $2-10i$ are plotted, as well as their corresponding image when multiplied by -1.
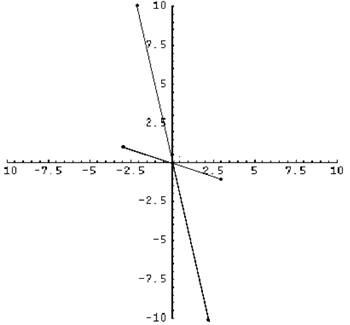
Our conjecture is that multiplying a point on the Argand diagram by -1 is equivalent to a 180 degree rotation about the origin.
Let $(a,b)$ on the Argand diagram represent the complex number $a+ib$, where $i$ is the square root of -1. So, multiplying $a+ib$ by -1, we get $-a-ib$, which is represented by the point $(-a,-b)$ in the Argand diagram. However, the point $(-a,-b)$ is a rotation of the point $(a,b)$ by 180 degrees about the origin. QED.
Using the same numbers for the second part, our conjecture here is that multiplying a complex number by $i$ gives a rotation of 90 degrees anti-clockwise on the Argand diagram.
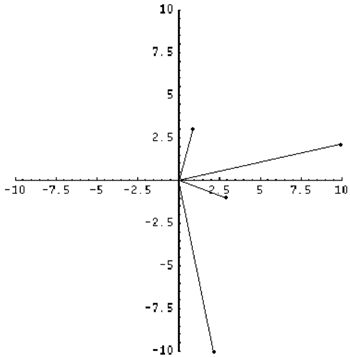
Again, assuming $(a,b)$ is a complex number plotted on the Argand diagram, by multiplying $a+ib$ by $i$, we get the complex number $-b+ai$, which is represented by the point $(-b,a)$ on the Argand diagram. This is equivalent to a rotation of 90 degrees anti-clockwise about the origin. QED.
Assuming we were to multiply the number by $i$ twice, this would give a rotation of 180 degrees (as shown in the first part because $i^2=-1$). Multiplying by $i$ thrice would be equivalent to a rotation of 270 degrees anti-clockwise, or 90 degrees clockwise and four time maps the number onto itself (essentially multiplying by 1). Multiplying by $i$ $n$ times is equivalent to rotating the point 90 degrees anti-clockwise $n$ times. Therefore; if $n$ is 0 mod 4, it has no effect; if $n$ is 1 mod 4, it's equivalent to an anti-clockwise rotation of 90 degrees; if $n$ is 2 mod 4, it's equivalent to a rotation of 180 degrees; if $n$ is 3 mod 4, it's equivalent to a rotation of 90 degrees clockwise.
NB. All these rotations are rotations of the initial point (a,b) about the origin as the centre of rotation.
Below the complex numbers $3-i$ and $2-10i$ are plotted, as well as their corresponding image when multiplied by -1.
Image

Our conjecture is that multiplying a point on the Argand diagram by -1 is equivalent to a 180 degree rotation about the origin.
Let $(a,b)$ on the Argand diagram represent the complex number $a+ib$, where $i$ is the square root of -1. So, multiplying $a+ib$ by -1, we get $-a-ib$, which is represented by the point $(-a,-b)$ in the Argand diagram. However, the point $(-a,-b)$ is a rotation of the point $(a,b)$ by 180 degrees about the origin. QED.
Using the same numbers for the second part, our conjecture here is that multiplying a complex number by $i$ gives a rotation of 90 degrees anti-clockwise on the Argand diagram.
Image

Again, assuming $(a,b)$ is a complex number plotted on the Argand diagram, by multiplying $a+ib$ by $i$, we get the complex number $-b+ai$, which is represented by the point $(-b,a)$ on the Argand diagram. This is equivalent to a rotation of 90 degrees anti-clockwise about the origin. QED.
Assuming we were to multiply the number by $i$ twice, this would give a rotation of 180 degrees (as shown in the first part because $i^2=-1$). Multiplying by $i$ thrice would be equivalent to a rotation of 270 degrees anti-clockwise, or 90 degrees clockwise and four time maps the number onto itself (essentially multiplying by 1). Multiplying by $i$ $n$ times is equivalent to rotating the point 90 degrees anti-clockwise $n$ times. Therefore; if $n$ is 0 mod 4, it has no effect; if $n$ is 1 mod 4, it's equivalent to an anti-clockwise rotation of 90 degrees; if $n$ is 2 mod 4, it's equivalent to a rotation of 180 degrees; if $n$ is 3 mod 4, it's equivalent to a rotation of 90 degrees clockwise.
NB. All these rotations are rotations of the initial point (a,b) about the origin as the centre of rotation.
Teachers' Resources
Possible extension
Try multiplying by $e^{{i\pi \over 3}} = {1\over 2} + i{\sqrt 3 \over 2}.$
