Transformations on a pegboard
How would you move the bands on the pegboard to alter these shapes?
Problem
Someone using an elastic band and a pegboard used four pegs to make the blue square you see below. They challenged another person to double the area by just moving two of the pegs. You can see what they did here.
Have a go at these:
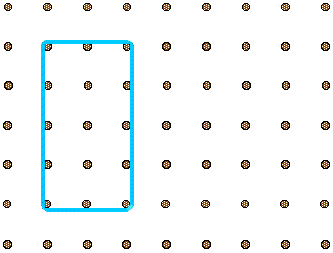
Can you make this into a right-angled triangle by moving just one peg?
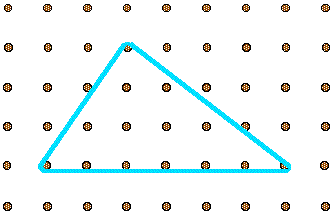
Can you enlarge this to the same shape with all the sides twice the length, moving just two pegs?
You could use our interactive geoboard below to try out your ideas.
Choose the size of your pegboard then select the line tool and click on two dots to draw a line between them.
You could set up some similar challenges for your friends, or have a go at More Transformations on a Pegboard.
Getting Started
Using a pegboard would be helpful, or if you don't have one, try using squared paper or this interactive geoboard.
What are the properties of a right-angled triangle?
Which peg have you tried to move?
Can you make the shape by moving a different peg instead?
Are there any other ways to do it?
Student Solutions
Isaac from Tockwith Primary Academy sent in the following:
I started off by thinking that you couldn't do it but then I thought that if I doubled the top units it would make four which was what I had on the sides. I doubled the sides to make eight units and that made the whole thing double the size. All I had to do was flip it round to fit on the board and I had done it.
Lillie sent in;
1)You start off with a 3x3 grid and you had to double it to make it 2x bigger you had to take the 2 pegs at the top and bottom of the right side and move them 2 gaps.
2) You have to start with a scalene triangle and change it to a right angle triangle you are only allowed to move 1 peg so you move the top peg and move it so it is in line with the bottom left peg.
3) You start off with the original shape and you count the gaps between each peg and on the bottom there were 2 gaps, and along the side there were 8 gaps you have to double each side and pull 8 gaps along the bottom and then do the same to the other side and you end up with the bottom being 4 and the sides being 8 but you don't have to double the bottom of the shape because you already have a side that is 4 gaps long.
Then Briony sent in;
1} On the first one what I did was started off with a 3 by 3 grid and moved the top left dome to the bottom left and moved it 2 gaps onwards and then I looked at what I did and I made a triangle.
2} You start with the original shape which is the triangle shape. So what I did was counted the gaps of the bottom bit which was 2, then I counted the side once which was 4, so 2 times 2 is 4 so I did 2 times 4 which makes 8. I moved the bottom right so it makes 8 gaps, then I moved the top right 8 gaps and it gave me my answer.
Lucy, who is educated at home, sent in a very clear solution to this question. For the first part she wrote:
You move the top peg to the right by one space. If you cut a square from all four corners, you end up with a quarter of it. In the middle of the square, you get four right angles.
I think there is at least one other way to get a right-angled triangle. Can you see how?
Lucy continued:
For the second problem, you know that the new shape is going to have sides $4 \times 8$ because the sides are multiplied by $2$. One of the sides is already $4$ so you just move the two right pegs $6$ spaces to the right.
Very well described solutions Lucy, thank you, and well done the other pupils.
Teachers' Resources
Transformations on a Pegboard
Someone using an elastic band and a pegboard used four pegs to make the blue square you see below. They challenged another person to double the area by just moving two of the pegs. You can see what they did here.
Have a go at these:
Can you make this into a right-angled triangle by moving just one peg?
Can you enlarge this to the same shape with all the sides twice the length, moving just two pegs?
You could use our interactive geoboard below to try out your ideas.
Choose the size of your pegboard then select the line tool and click on two dots to draw a line between them.
You could set up some similar challenges for your friends, or have a go at More Transformations on a Pegboard.
Why do this problem?
This problem is a good way of consolidating properties of shapes and visualising changes in their properties. The interactive enables learners to satisfy their curiosity and try out ideas, when at first the task might seem very challenging.
Possible approach
Learners could draw their answers on square dotty paper or write instructions in words (which is much harder!).
Key questions
Possible extension
Learners could make up similar puzzles for others to do using the virtual geoboard or paper. They may also like to have a go at the challenge More Transformations on a Pegboard which focuses on areas of triangles.
Possible support
Using a real pegboard with elastic bands will make this more accessible for many children. They could use two bands in different colours so that one can be left in the original place all the time.