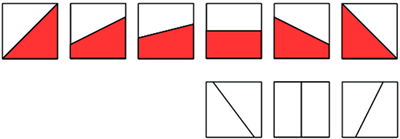
Halving
These pictures show squares split into halves. Can you find other ways?
Problem
These images show squares split in half:


Getting Started
Have you thought about using the squares on your squared paper to help you check your drawings?
How about cutting out your square? How would this help to check that you had divided it in half?
Student Solutions
Aoibheann and Padriac from Cloghans Hill NS in Ireland, said:
You can check that the squares are properly halved by cutting out the pieces and assembling them back to back or on top of each other, manipulated so they are the starting in the same places.
Very well explained, thank you.
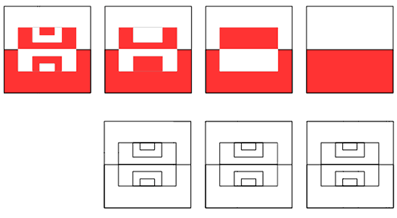
Other ways to do halves are included in the photo they sent:

These ideas were sent in by Donna of Zion Heights.
To check that each way is correct, you can measure the area of each red/white piece and see if the combined total area of the white pieces is equal to the total area of the red pieces. You can also cut out the white and red pieces and see if you can rearrange them so that every white piece has a matching, congruent red piece.
Here are two more possible ways to cut a square in half:
Krystof also sent in another way to cut a square in half:
Thank you to all of you.
Yusuke and Alex from the United World College of South East Asia East Campus wrote
Some of them are not in equal halves like the other ones on the top. The half on the right bottom side is a equal half. I know this because halves have to be equal and symetrical in any way.
Dylan from St Louis de Monfort in Australia wrote
To start with, a straight line down the middle can easily be seen as even however when there are harder shapes like when the amount of red and the amount of white are in totally different spots then it can get challenging. By simply checking that the shape is symmetrical then you can safely assumethat they are even
Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.
Thank you for those of you who sent in your ideas and thoughts.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Some children might enjoy investigating how to split other shapes in half. They could try Happy Halving which involves doing just that.
Possible support