Snookered
In a snooker game the brown ball was on the lip of the pocket but
it could not be hit directly as the black ball was in the way. How
could it be potted by playing the white ball off a cushion?
Problem
At a recent snooker competition, one player found herself faced with the situation below:
Image
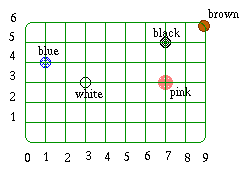
Her next shot was the brown ball which was nicely positioned on the lip of the pocket. Unfortunately she was unable to hit the brown ball directly as the black ball was in the way.
- Could she pot the brown ball by playing the white ball off only one cushion?
- Could she pot the brown ball by playing the white ball off two cushions?
- What are the coordinates of any points on the cushion that she could aim for to pot the brown ball?
Getting Started
If you draw copies of the table reflected in the cushions then the reflection of the path of the ball after hitting a cushion appears as a straight line in the image of the table.
Image

Student Solutions
A number of correct answers to the above were received which included:
- The brown ball cannot be potted off just one cushion.
-
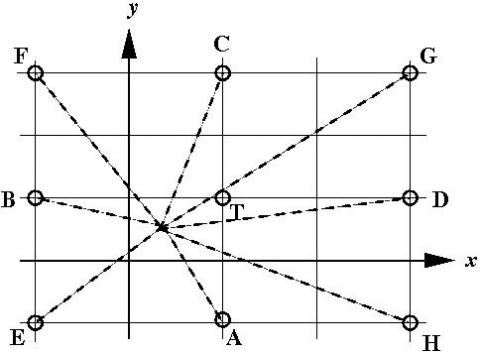
Playing off two cushions the brown ball can be potted off two cushions in three ways. The three points that must be aimed at have coordinates (4.2, 6) (9, 3.75) and (0, 0.75)The diagram shows the snooker table and 15 copies of the table. The path of the ball after bouncing off a wall (reflection) is shown by a straight line in the adjacent copy of the table.Image
The snooker table is bounded by the lines $x=0$, $x=9$, $y=0$ and $y=6$.
The white ball is at W(3, 3), the brown (target ball T) is at (9, 6), the pink is at (7, 3), the black is at (7, 5) and the blue is at (1, 4).With no other balls in the way, travelling initially in the direction WA or WB, the white ball would hit the target having bounced off one wall.With no other balls in the way, travelling initially in the direction WC, WD or WE, the white ball would hit the target having bounced off two walls.With no other balls in the way, travelling initially in the direction WF or WH, the white ball would hit the target having bounced off three walls and in the direction WG it would bounce off 4 walls.This pattern can of course be extended in all directions to show bouncing off 4 or more walls.
OA has gradient ${-3\over 2}$ and goes through the point (7, -3) so the pink ball at (7, 3) would be in the path of the white ball.
OB has gradient ${-1\over 4}$ and goes through the point (-1, 4) so the blue ball at (1, 4) would be in the path of the white ball.
OC has gradient ${5\over 2}$ and hits the first wall at (4.2, 6) bouncing off two walls parallel to the x axis before hitting the brown ball. None of the other balls is in its path.
OD has gradient ${1\over 8}$ and hits the first wall at (9, 3.75) bouncing off two walls parallel to the y axis before hitting the brown ball.
OE has gradient ${3\over 4}$ and hits the first wall at (0, 0.75) bouncing off two walls, one parallel to the y axis and one to the x axis, before hitting the brown ball.
OF has gradient ${-5\over 4}$ and hits the first wall at (0.6, 6) bouncing off three walls before hitting the brown ball.
OG has gradient ${5\over 8}$ and hits the first wall at (7.8, 6) bouncing off four walls before hitting the brown ball.
OH has gradient ${5\over 8}$ and hits the first wall at (9, 0.75) bouncing off three walls before hitting the brown ball.
Teachers' Resources
Why do this problem?
The problem develops visualisation. Students may be interested because snooker is a popular game and they may be impressed that expert players can judge the angle of the shot accurately to bounce of two, three or even 4 walls and hit the target. One way to solve the problem is to use coordinates, similar triangles and gradients.
Possible approach
Work through one of the cases as a class together and then suggest that students draw a diagram. Then discuss the diagram as a class before the students calculate the various paths.
Key question
How can we turn into a straight line the path and the reflected path after the ball bounces off a cushion?
Possible support
Initially ignore the pink and blueballs which might be in the way of the shot.
See also Cushion Ball which has an interactivity.
Possible extension
See the article In Space Do All The Roads Lead Home?
