Three Way Mix Up

We received several different arrangements of tiles - thank you to those who sent in your suggestions. You had to remember that you didn't necessarily need one tile of each colour in every row and column - it was just that tiles of the same colour weren't allowed to touch. Not many of you looked for more than one other arrangement but Kesavan from Latymer All Saints C of E Primary sent in these solutions:

Louise from Farnborough Hill sent these arrangements:

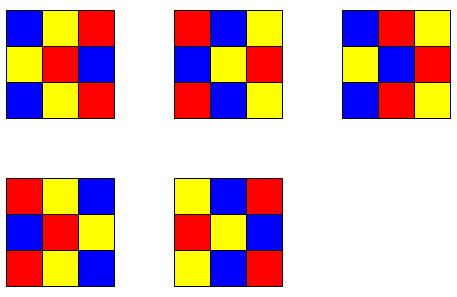
Trish and James sent in their solutions:

We put all the blues on the diagonal, so none of them were touching, and then we put a red in one corner and a yellow in the other so they weren't touching and then we had to put the other colours where they are. Then we did the same with a red diagonal and a yellow diagonal:

A great way of working out some possible results!

Finding all the possible arrangements of tiles is quite a challenge and some of you began to have a go at this. Danny told us how he worked out how many possible combinations there were:

First I worked it out starting with blue in the top left corner and red next to it in the top middle.

There are six different ways of starting (blue then red, blue then yellow, red then blue, red then yellow, yellow then red, yellow then blue) so there will be six times as many answers as I got starting with blue then red. This is because if I take one answer and swap all the blues for yellows and yellows for blues I get another answer, and there are six different ways to swap the colours.

The two squares below the starting two can be yellow then blue, red then blue or red then yellow. That way I had three different ways the top left two by two squares could be coloured.

Then I worked out how many different ways you can colour in the top right and middle right squares.

There are three ways for each of the different starting two by two squares.

For instance for the starting two by two squares with yellow then blue on the second row, here are the first and second rows of the whole arrangement:

Then I worked out how many ways the bottom squares can be coloured and I think there are a total of three ways which work with this arrangement of the top left two by two square.

Then I looked at the arrangements of still having blue and red in the top left and top middle, but this time with red and blue underneath them, but none of these worked.

Finally, I looked at the arrangements of blue and red in the top left and top middle with red and yellow underneath them and I found another three ways.

So, I think there are six different ways of starting with blue then red, so there must be thirty six different ways altogether.

Thank you, Danny!

However, Suzanne, working with her son Lawrence at home, wrote to us to say:

We have just been doing 'Three Way Mix Up' and our solution is a little at odds with the solution published.  Danny suggests that there are 6 ways of starting namely blue, red; blue, yellow; red, blue; red, yellow; yellow, blue and yellow red.  So far so good.  However he then works out that there are 6 possible permutations for each starting pair. Not so - there are only 4.  If you look at the illustration of his solution, the middle one i.e. blue, red, blue  then yellow, blue, red, has no possible third row without 2 yellows being next to each other.  Therefore there are only 4 possible permutations for each of his starting duos.

Thank you for pointing this out, Lawrence and Suzanne!

We used a different approach. Using coloured milk carton lids and moving them round, we looked at the different patterns possible and discovered that there were two basic patterns - chevrons and diagonals.  We then worked out all the possible colour combinations for each pattern.  This does indeed give you 36 possible combinations but we worked them all out to be sure.

Here is a picture of some of their possible combinations:



They sent the following explanation about the pictures:

Diagonals yellow, red then blue going both ways with both different permutations of the other two colours  (3 x 4).
Then the chevrons red/yellow and yellow/red going L to R, R to L, top to bottom and bottom to top  (2 x 4 = 8). 
Then for the other two chevron colour combinations  blue/red and red/blue then blue/yellow and  yellow/blue we have only included the basic pattern  (L to R), each of which is multiplied by 4 for the four different directions. 
So 3 x 8 chevron combinations.
Hope this makes sense!

I like the chevron and diagonal idea - thank you to you both for sending in your thoughts.