LOGO challenge 2 - diamonds are forever
The challenge is to produce elegant solutions. Elegance here implies simplicity. The focus is on rhombi, in particular those formed by jointing two equilateral triangles along an edge.
Problem
It is useful to feel comfortable using procedures, though if you have not met procedures before- this might help you feel why they might be useful. More about procedures can be found in FIRST FORWARD 6 and in the next challenges.
The challenge is to produce elegant solutions to the problem. Elegance here implies simplicity. The focus is on rhombi. Or:
REPEAT 2 [ FD 40 RT 60 FD 40 RT 120]
The design below is part of tile seen in a shop - sadly now closed, at King's Cross in London. Can you generate it in as elegant a fashion as possible?
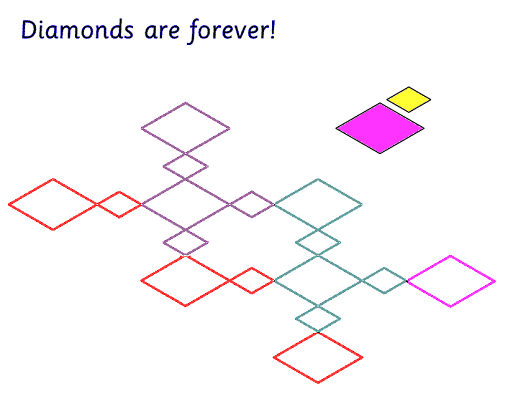
You can download some excellent free LOGO software from the internet at http://fmslogo.sourceforge.net/.
Teachers' Resources
There are many ways to tackle the challenge.
You might like to consider returning to this challenge when you have found out about procedures. For now you might like to see how you might use the REPEAT command.
Here are some ideas:
- Can you draw one rhombus?
- Can you write a single line of code that draws the two rhombi joined together?
