Going Deeper: Achieving Greater Depth with Geometry
Developing fluency, reasoning and problem solving are the three key aims of the primary maths curriculum in England (DfE, 2013). However, arithmetic fluency tends to dominate in many classrooms. This is despite research indicating that reasoning skills having a greater impact than arithmetic fluency on mathematical attainment among 7-11 year-olds (Nunes et al, 2009).
Moreover, the same research team also noted that the spatial skills required to rotate and manipulate shapes, and imagine the results of these actions, are key indicators of later mathematical achievement. Therefore developing and embedding geometrical skills and knowledge arguably deserves a much more prominent role in the primary maths classroom.
This article explores how learners can ‘go deeper’ with primary geometry by:
- solving problems of greater complexity (where the approach is not immediately obvious), demonstrating creativity and imagination;
- communicating results clearly and systematically to explain and generalise the mathematics.
(Askew et al. 2015, p.7)
We will begin by offering a selection of activities across the primary age range which enable young learners to 'go deeper’ by solving unfamiliar problems that develop spatial awareness. (These activities are also featured in the NCETM's ready to Progress materials.) We will then follow with a discussion of meaningful ways in which young learners can develop their mathematical communication skills (including submitting work for possible publication on the NRICH website).
Solving unfamiliar problems
Key Stage 1 (5-7 year-olds)
You could begin by allowing children time to look carefully at the shapes and part-shapes on their own cards and to describe what is on their own cards without showing them to others. After a suitable time, encourage them to ask each other about the other cards. You could suggest that one child chooses a card to describe to the others in the group and the others try to draw what is being described. Once they have successfully completed the challenge as written, they could go even deeper still by devising their own version for other learners.
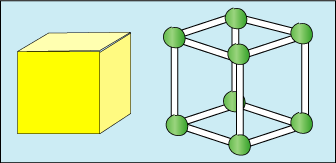
Skeleton Shapes also helps to promote discussion and experimentation in the primary classroom. Naming the shapes should help during discussion and description of what has been done, rather than being an exercise in its own right. We have found that learners can 'go deeper' by comparing different ways to record their findings, including the use of diagrams, tables and photos.
Key Stage 2 (7-11 year-olds)
Geometry has a precise language, and young learners need time to understand the similarities and differences between different shapes. Activities such as Seeing Squares and Square Corners enable them to understand that squares do not necessarily have to be orientated so that their sides are horizontal and vertical:
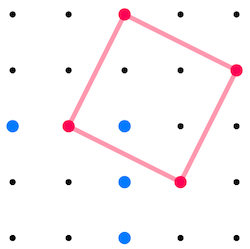
The shape above is still a square (as opposed to a diamond!). The playful context of these activities encourages learners to 'go deeper' as they explore the different squares they can draw on a grid.
Comparing shapes often forces young learners to become much more precise in their use of mathematical vocabulary. Our Egyptian Rope challenge offers the opportunity to compare different 2D shapes using a historical context. Initially, learners are invited to explore the triangles they can make from a piece of rope which has been knotted to make twelve equal sections (there must be a knot at each corner). They are then encouraged to create regular polygons. In our Stringy Quads task, groups of young learners are invited to stretch a piece of string out so that each of them is holding a corner to make a quadrilateral. They are challenged to make a quadrilateral which has exactly one line of symmetry and 'go deeeper' by convincing someone else that they are right.
Taking things further, learners can 'go deeper' by making connections in their learning too. A Cartesian Puzzle gives coordinates of eight quadrilaterals, but in each case one coordinate is missing. Learners are challenged to work out the missing coordinates, given that all the quadrilaterals have line symmetry, or rotational symmetry, or both. The task requires children to have some understanding of coordinates in the first quadrant and calls on their knowledge of symmetry, and the properties of various quadrilaterals.

Bringing everything together, Shape Draw is an ideal group task for 'going deeper' which helps to consolidate learners' understanding of properties of quadrilaterals, area, perimeter and symmetry. It offers a useful assessment task for either before or after a teaching sequence focusing on geometry. It also provides a context in which to encourage young children to approach a task flexibly, in this case by being open to adapt their solution to fit all the criteria as more information becomes available.
So far, we have focused on solving unfamiliar geometry problems, which is one of the two key aspects of ‘going deeper’ we are exploring in this article. We will now move on to looking at ways of developing mathematical communication skills in the primary classroom.
Encouraging more meaningful mathematical communication
It has been suggested by prominent mathematics educator John Mason that there are three levels of convincing in mathematics – convincing yourself, convincing a friend and convincing a sceptic (2000). Sometimes even the first level can be a real challenge, especially for less confident learners. Encouraging them to justify their answers, share their thinking processes and present their findings for friends can help them to further develop their communication skills.
At NRICH, we provide opportunities for learners to convince a sceptic by inviting them to share their thinking about our latest Live Problems with our team. We later publish a selection of the solutions we receive for each activity in the ‘Student Solutions' tab. These solutions often offer incredibly useful examples of 'going deeper' in the classroom.
For example, we've discussed how learners might record their solutions to the Skeleton Shapes activity in different ways to convince others that they've found all possible solutions. Pupils from Histon and Impington Infant School sent in this photo to convince others of their solution:

A willingness to explore more than one possible answer is often a feature of the solutions chosen for publication on NRICH. Here's an excerpt from a solution submitted for our Stringy Quads investigation where learners Matthew and Jordan demonstrated their knowledge of the properties of shapes, and willingness to 'go deeper' by exploring more than one possible answer:
We made three lots of triangles. We made an isosceles triangle with 2, 5 and 5. Then we made an equilateral triangle with three lots of 4. The last triangle was a right angled triangle with 5, 4 and 3. We made two rectangles one had 4, 2, 4, 2. The last rectangle had 5, 1, 5, 1. The square had 3, 3, 3, 3. Then we made a hexagon and it had 2, 2, 2, 2, 2, 2.
Encouraging students to work systematically can enable them to 'go deeper' too. Here is a solution sent in by Will, Hugh, Emil and Ben from Oare Primary School who clearly explained their systematic approach to the Stringy Quads challenge:
1] Firstly, we got a ball of string and rolled it out so we could each hold a corner and we cut it.
2] Next, we thought up a shape with four corners [quadrilateral]. We thought of two: a trapezium and a kite. To persuade people, you draw a kite, and tell people to draw all the lines of symmetry and there should be one.
3] A shape [quadrilateral] with only two lines of symmetry is an oblong. To prove it only has two lines, you repeat the same method as last time but with two lines of symmetry.
4] It is not possible to have a quadrilateral with three lines of symmetry, because you can't divide 4 by 3.
5] A square is a shape with four lines of symmetry.
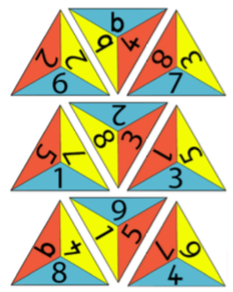
Another excellent activity for encouraging learners to 'go deeper' by working systematically is One Big Triangle, where learners have nine small triangles to rearrange into one larger triangle so that all the numbers that touch total ten.
Ryan from Hayton Primary in Cumbria shared his systematic approach with our team:
I started working from the top to the bottom with a small triangle.
I worked downwards to test out which was the right triangle to go at the top.
It took me about five tries to get the right triangle at the top.
When I got the right triangle at the top, all the other triangles were easy to fit in, working top to bottom.
Our Always, Sometimes, Never shape activities offer an excellent opportunity for learners to begin to explore counter examples. For example, Eira from Tywford School shared her thoughts about the statement 'The base of a pyramid is square':

Let's Investigate Triangles is a playful context in which learners can explore whether or not strips of different lengths (from a construction set) can make triangles. Children have the chance to find multiple solutions and non-solutions, notice patterns and articulate these patterns for others to see. They can then begin to explain why the patterns occur, which could lead to a generalisation. The interactivity in this task makes it accessible to all children, whether or not the practical equipment is available. (Although of course we would advocate using the 'hands-on' equipment if possible.)
Being able to submit solutions to NRICH can be a huge motivator for some learners - it provides 'a reason to reason'. As you can see from the above, the opportunity to share solutions on NRICH encourages children to work at a greater depth by convincing others, making connections, working systematically and developing a willingess to explore more than one possible solution. To help young learners, and their teachers, better understand what we are looking for in a solution, and the various different ways that they can share their work, we have published some useful guidance.
In conclusion
We hope that these geometrical activities, and others on the NRICH Primary curriculum mapping document, will enable learners to develop the reasoning, spatial and communication skills needed to 'go deeper' with geometry throughout their primary years.
References
Askew, A., Bishop, S., Christie, C., Eaton, S., Griffin, P. and Morgan, D. (2015) Teaching for Mastery: Questions, tasks and activities to support assessment. Oxford University Press.
DfE (2013) Mathematics programmes of study: Key stages 1 and 2 National Curriculum in England. Department for Education.
Mason, J. (2000) Learning and doing mathematics (2nd ed.). Tarquin Publications.
Nunes, T., Bryant, P., Sylva, K. and Barros, R. (2009) Development of maths capabilities and confidence in primary school. Department for Children, Schools and Families.