True or False?
Problem
The idea of this activity is for you to decide whether each of the number sentences below is true or false.
Try not to use written calculations if you can, and if possible, talk to someone else about your ideas.
When you are ready, click below to see the number sentences. (Alternatively, you could download this sheet which contains all the number sentences. You could print it out and cut it up so that each number sentence is separate.)
We would love to hear about your reasoning. How do you know whether a particular number sentence is true or false?
a. 19 + 15 = 34
b. 34 = 19 + 15
c. 19 + 15 = 15 + 19
d. 34 = 34
e. 19 + 15 = 34 + 0
f. 19 + 15 = 0 + 34
g. 34 = 16 + 17
h. 19 + 15 = 21 + 13
i. 19 + 15 = 20 + 16
j. 19 + 15 = 22 + 18
k. 19 + 15 = 34 + 15
l. 15 + 19 = 20 + 14
For a further challenge, take a look at the number sentences below, or on this sheet.
Which are true? Which are false? How do you know?
Are you able to decide without doing any calculating?
a. 346 + 289 = 349 + 286
b. 727 + 581 = 581 + 727
c. 478 - 192 = 480 - 194
d. 831 - 344 = 841 - 334
e. 346 + 289 = 345 + 288
f. 727 + 581 - 581 = 727
g. 831 - 344 + 346 = 831
h. 169 + 672 = 2041
You might like to use the balance interactivity below to help you make decisions, and/or to check your conclusions.
You can use the calculator tool to create one side of a number sentence.
Pressing 'OK' puts that part of the number sentence into a box which you can drag to one side of the balance.
Getting Started
What does the equals sign mean?
Rather than calculating, can you compare the two sides of the equals sign with each other?
Student Solutions
Thank you to everybody who sent in their ideas for this task. We received a lot of solutions from children at the British International School in Vietnam and from children at the ABQ Education Group in Oman, as well as children at Pierrepont Gamston Primary School in England. Well done to those children and to everybody else who sent in their reasoning for why each number sentence was true or false.
Juyeong from Nord Anglia School Jakarta in Indonesia explained the technique they used to solve the questions:
I solved them using the things that I already know and the things that I already can do.
What I know that will be useful to solve it is that = means the same and 19 + 15 which is the basic adding of this question is 34.
Well done Juyeong - with questions like these, it can be really helpful to think about which facts we already know.
Avneet from Pierrepont Gamston Primary School worked out all the combinations of two numbers that add up to 34:
Questions 1-6 are all correct. I have concluded that the only possible solutions for _+_=34 (without decimals or negative numbers) must be 1+33, 2+32, 3+31, 4+30, 5+29, 6+28, 7+27, 8+26, 9+25, 10+24, 11+23, 12+22, 13+21, 14+20 and 15+19. This is why questions 7, 9, 10 and 11 are wrong and 8 and 12 are right.
This is a really interesting way of thinking about it, Avneet. Have a look at these additions - can you see any other ways of making 34?
Gracie and Georgie from Horfield CEVC Primary School in the UK have looked closely at how adding and subtracting from two numbers can keep the total of the numbers the same:

Thank you both for sending us your ideas. Have a look at the rest of Gracie and Georgie's solutions for some very clear explanations of why each statement is true or false.
Anika from Holy Family Catholic Primary School in England has used some similar strategies to Gracie and Georgie. Anika has also looked at the last digits of each of the numbers to decide whether the calculation can be true or not:
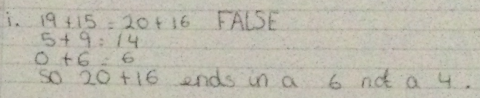
Thank you for sending us your ideas - we've uploaded a picture of the rest of Anika's solutions.
Jannah from the ABQ Education Group sent us this video explaining why each number sentence is true or false in the extension activity:
Jannah also explained that the video got cut off before the end, but that the last number sentence has to be false because the two numbers on the left aren't very big numbers so they can't possibly equal 2041. Thank you for that video, Jannah!
Isabelle from Nord Anglia School Jakarta has also used looked at the size of the numbers to answer some of these questions:
a. True, because 346 + 3 = 349, and 289 - 3 = 286, so both of the answers of the equation will be equal = 635 (346 + 289 = 349 + 286).
b. True, because they are the same equations, they just swapped the numbers' order. So, 727 + 581 = 581 + 727 = 1,308.
c. True, because 478 + 2 = 480, and 192 + 2 = 194, so the answers will be the same or equal, 478 - 192 = 480 - 194 = 286.
d. False, because the equation on the left will have a smaller answer, because 831 is smaller than 841, but the 344 is greater than 334, so the answer for the equation on the left will be smaller than the answer for the equation on the right. (831 - 344 = 487 is smaller than 841 - 334 = 507).
e. False, because the first sum on the left will have a greater number, because 346 is greater than 345, and 289 is greater than 288, so 346 + 289 = 635 is greater than 345 + 288 = 633.
f. True, because 581 - 581 = 0, so 727 + 0 = 727.
g. False, because -344 + 346 = 2, so it means that 831 + 2 = 833 not 831 and you can also say that -344 + 346 = 2, not 0.
h. False, because 169 + 672 is definitely less than 1,000; the answer would be 841. So, 169 + 672 = 841, not 2041.
Well done Isabelle!
Luay from Goldsworth Primary School in the UK used real-life examples to explain some of the questions:
Q6) 727 + 581 - 581 = 727
A6) True. My sister has y amount of chocolates. I have x amount of chocolates. I put my x amount of chocolates next to my sister's y amount. Then I take my x amount of chocolates back home for no actual reason. So she has her original y amount left.
Q7) 831 - 344 + 346 = 831
A7) False - There is z amount of chocolates. 344 is taken away from that and 346 is added back which 2 more than what was taken away. So z becomes z + 2 which means you would have 2 chocolates more than what you had
initially.
This is a really helpful way of imagining what it means to do a combination of adding and subtracting in a number sentence - well done.
We also had an excellent solution sent in by Simran from Maurice Hawk School in the USA. Thank you again to everybody who sent in their ideas for this challenge.
Teachers' Resources
Why do this problem?
This task will help you unpick children's understanding of the equals sign. It may reveal misconceptions and help you to address them.
This problem and the possible approach below have been inspired by the book 'Thinking Mathematically' written by Carpenter, Franke and Levi (2003). The full reference is included at the foot of this page.
Possible approach
This problem featured in an NRICH Primary webinar in January 2021.
Carpenter et al.'s research found that many teachers were surprised by their class' responses to these kind of calculations, sequenced in the way described below. So, before having a go at this task with your class, it might be useful to consider how you think your children might respond.
To introduce this task, write 19+15=34 on the board. Invite learners to decide whether it is true or false, and why, firstly by giving some individual thinking time and then by asking everyone to share their ideas with a partner. Invite a pair to explain their conclusions to the whole group. You could then ask whether other pairs used a different approach to decide, and share a few alternative ways.
Next, write 34=19+15 on the board (leave the first calculation visible too), and again ask whether it is true or false, and why. As pairs are discussing their thoughts, listen out for their assertions and accompanying reasoning. You may wish to invite each pair to indicate their conclusion to you in some way e.g. by discretely putting a thumbs up or a thumbs down. If there is disagreement, choose a pair to explain why they think 34=19+15 is false. This may reveal some assumptions about the equals sign. Some learners believe that there can only be a single number after the equals sign and/or that an equals sign means 'the answer comes next'. Encourage other members of the class to comment on, or ask questions about, any reasoning that is verbalised.
Depending on the responses to the second example, you may like to offer a third example on the board for everyone to consider, or you may prefer to give pairs these cards, which include all the calculations in the first set. If the latter, allow time for all pairs to decide whether each number sentence is true or false, and why.
Draw the whole group together to share their thoughts. Again, try to facilitate a whole class discussion rather than you being the one to comment on or validate children's contributions. Encourage learners to see the equals sign as representing a relation between two equal numbers, in other words meaning 'the same number as'. Choosing words that express the relationship clearly can really help learners. For example, "34 is the same amount as 19 plus 15".
At this point you could offer children the second set of number sentences to further consolidate and develop their understanding. This second set encourages learners to see the relationship between the left and right sides of the equals sign by including number sentences in which the left and right hand sides can be compared with each other, without the need to do any calculation. For example, listen out for learners who know that 346+289=349+286 is true by reasoning that 349 is three more than 346 but 286 is three less than 289, so the amount on each side of the equals sign is the same.
Throughout the lesson, you may choose to use the interactivity as a way of visually checking children's solutions, or even challenging their answers.
Key questions
How would you 'read out' this number sentence? What does that mean?
Why do you think this number sentence is true/false?
Possible support
It may be useful to sit alongside some learners and listen in to their conversation, and gently offer questions and prompts to probe further. You can then deliberately offer a particular number sentence next, which might help them grapple with any misunderstanding. For example, if a pair is adamant that there can only be one number after an equals sign, try offering them the number sentence 19+15=34+0 next.
Possible extension
You could invite learners to create their own set of true or false number sentences for a partner to try. You might specifically ask them to include examples where they think that calculation is unnecessary. This is a great way to reveal their understanding of relations.
Reference:
Carpenter, T. P., Franke, M. L. and Levi, L. (2003) Thinking Mathematically: Integrating Arithmetic and Algebra in Elementary School. Portsmouth, NH: Heinemann.
