The Best Card Trick?
Time for a little mathemagic! Choose any five cards from a pack and show four of them to your partner. How can they work out the fifth?
Problem
Can you use it to make sense of the code?

This trick first appears in Wallace Lee's book "Math Miracles" in which he credits its invention to William Fitch Cheney, Jr., a.k.a. "Fitch."
You can read an article by Michael Kleber, the first part of which describes the trick, here.
Getting Started
Here are a few examples:
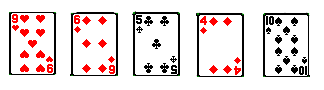
If we are dealt 3S, 5S, 3D, 4C, 9H:
Place 3S down first (to indicate that the secret card is a spade),
then 3D, 9H, 4C (low, high, middle)
to indicate that the secret card is 2 more than the 3S, i.e. the 5S.
If we are dealt 3S, 9S, 3D, 4C, 9H:
Place 3S down first (to indicate that the secret card is a spade),
then 9H, 4C, 3D (high, middle, low)
to indicate that the secret card is 6 more than the 3S, i.e. the 9S.
If we are dealt 3S, 10S, 3D, 4C, 9H:
Place 10S down first (to indicate that the secret card is a spade),
then 9H, 4C, 3D (high, middle, low)
to indicate that the secret card is 6 more than the 10S, i.e. the 3S.
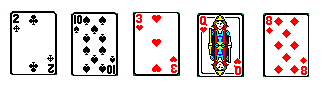
If we are dealt 2H, JH, 4D, 4C, 4S:
Place JH down first (to indicate that the secret card is a heart),
then 4D, 4S, 4C (middle, high, low)
to indicate that the secret card is 4 more than the JH, i.e.the 2H.
Student Solutions
James, from Hampton School, gave us his ideas on how to order the cards to show to his partner:
For the first set of 5 cards, the two cards with the same suit are the diamonds: the 4d should be the "base" card as the gap between the 4d and the 6d is 2, which can be expressed using the remaining three cards with l h m. Therefore, from right to left, the cards would be the 4 of diamonds followed by the 5 of clubs, the 10 of spades and the 9 of hearts, allowing you to guess the 6 of diamonds.
Jamie and Monty from Hurstpierpoint Prep School came to the same conclusion.
Aswaath, from Garden International School, Kuala Lumpur, sent us his thoughts on how he would show his partner the cards:
For the first set of cards, I would place four cards in this particular order: 4d, 5c, 10s and 9h. I would keep 6d the secret card.
For the second set of cards, I would place four cards in this particular order: Qh, 8d, 10s and 2c. I would keep 3h the secret card.
For the third set of cards, I would place four cards in this particular order: 7h, 7s, 7d and 7c. I would keep Kh the secret card.
Great - you all seem to have understood Charlie's crib sheet well!
Teachers' Resources
Why do this problem?
This is an engaging activity in which students are given information and expected to make sense of it. It may lead to a discussion of modular arithmetic.
Possible approach
The video, or a live performance of the trick with a colleague, provides a hook to draw students into the problem.
Perform the trick three or four times, keeping a record of the four cards and the secret card. Ask them to discuss in pairs any ideas they might have about how the trick is done.
Share as a class any ideas that emerge and give students the chance to try out any suggestions with a pack of cards.
It is quite likely that the strategy used in the video won't emerge, so once students have appreciated the limitations of their suggested methods, hand out this worksheet. Give students time to make sense of the instructions and to perform the trick in pairs a few times. Ensure that they swap roles and have experience of both selecting the cards and 'guessing' the secret card.
"At the end of the lesson I am going to choose one of you at random and give you five cards. You will choose four cards to show to the rest of the class and I will expect everyone to be able to predict what the fifth card is!"
Finally you may want to discuss why the trick always works.
Possible extension
Four cards can be arranged in $4 \times 3 \times 2 \times 1 = 24$ ways. There are 52 cards in a pack. How can these 24 possibilities convey enough information to distinguish between 52 different cards?
Possible support
There are some worked examples in the Hint.
