About Pythagorean golden means
We shall show that there is a simple and perhaps unexpected relationship between the arithmetic, geometric and harmonic means of two numbers, the sides of a right angled triangle and the Golden Ratio.
First we'll define these terms and then indicate a simple proof of the formula which connects them all. As usual with NRICH articles, we'll leave readers a little work to do for themselves so we suggest you find a pen and paper.
Take any two numbers $a$ and $b$, where $0 < a < b$. The arithmetic mean (AM) is ${1 \over 2}(a+b)$; the geometric mean (GM) is $\sqrt{ab}$; and the harmonic mean (HM) is the reciprocal of the arithmetic mean of the reciprocals of the numbers. The HM is $${1\over {1\over 2}({1\over a} + {1\over b})}$$ which simplifies to $2ab/(a+b)$.
Consider the circle centre A and the tangent to the circle from the point M touching the circle at the point G with PM =$a$, QM = $b$ and $a > b > 0$. You can work out the radius of the circle and show the length AM is $(a+b)/2$ (the arithmetic mean of $a$ and $b$). Using Pythagoras' theorem you can show the length GM is $\sqrt{ab}$ (the geometric mean of a and b). Using the fact that the triangles AGM and GHM are similar you can show that HM is $2ab/(a+b)$ (the harmonic mean of $a$ and $b$).
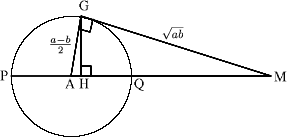
The diagram shows that AM > GM > HM .
The Golden Ratio is said to give aesthetically pleasing proportions when you take a rectangle which is such that if you remove a square from it you have a rectangle of the same proportions.
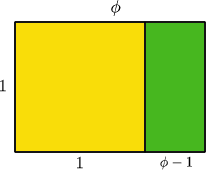
The Golden Ratio $\phi$ is such that $\phi \ : 1 = 1 : (\phi \ - 1) $ so that $\phi^2 - \phi \ - 1=0$ and hence $\phi = {1\over 2} (1 + \sqrt{5})$.
In the diagram above used to illustrate the inequality AM > GM > HM these three lengths did not appear in the same triangle. It can be shown that the AM, GM and HM of $a$ and $b$ can be the lengths of the sides of a right-angled triangle if and only if \begin{equation*} a = b\phi^3 \end{equation*}
where $\phi = {1 \over 2}(1+\sqrt{5})$ , the Golden Ratio.
All you need to do to prove this remarkable result is to use elementary algebra to find $a/b$ where $[AM]^2 = [GM]^2 + [HM]^2$, that is
$$ \left[{(a+b)\over2}\right]^2 = \left[\sqrt{ab}\right]^2 + \left[{2ab\over(a+b)}\right]^2. $$
The details of this proof are given in the solution to the problem Pythagorean Golden Means.
