Counting Stick Conjectures
Problem
Have you ever seen a counting stick? You might have one in your classroom at school. Here is a photo of one:
What do you see?
What do you notice?
What would you like to ask?
Here is a simple picture of the counting stick:
How many rectangles can you see? (The rectangles may be different sizes.)
Once you've had a think about how many rectangles there might be, click below to see what Zoya thought.
Zoya says:
"I can see some small rectangles, which are either yellow or blue.
I can also see some bigger rectangles, made of two of the small ones. And some that are even bigger too.
I tried to count all the rectangles but I got very confused."
What might you suggest that would help Zoya?
Again, have a think and then click below to see what Max suggested.
Max says:
"Perhaps it would be easier if we started with a smaller counting stick.
We could try a counting stick with just two of the smallest rectangles, like this:
I think that has two small rectangles and one larger one, which makes three rectangles altogether.
Then we could try a counting stick with three smallest rectangles, like this:
This time I can see three very small rectangles, two blue and one yellow.
I can also see a rectangle which is made up of two of these small ones, which I've outlined in red:
And there's another one like this:
And then there is one large rectangle:
So, I think that makes six altogether.
If we do this a few more times with different sized sticks, perhaps we'll see a pattern."
Can you see how Max worked out the total number of rectangles each time?
Try out his suggestion. How many rectangles are there on a counting stick which is made up of four small squares? Five squares? Six...?
What do you notice? Can you see a pattern?
Is there a quick way to work out how many rectangles there would be, for a counting stick with 100 sections? Or 1000? Or...
How can you be sure that what you have noticed will always be true?
Mathematicians aren't usually satisfied with a few examples to convince themselves that something is always true.
Can you provide an argument that would convince mathematicians?
Getting Started
How many of the smallest rectangles are there in your stick?
How many rectangles that are 'two small rectangles long' are there in your stick? How many that are 'three small rectangles long'? ...
How are you keeping track of your total so far?
Student Solutions
Well done to everybody who investigated the number of rectangles inside a counting stick. We received a lot of solutions to this activity and unfortunately we don't have space for all of them here. Thank you to all the children at Highgate Junior School in the UK who sent in their ideas, and thank you as well to Ryan from Kong Hwa School in Singapore, Lawrence from YCIS in China, and Amy and Teija from Pierrepont Gamston Primary School in England. You all had some great suggestions similar to the ones we've featured below.
Melissa from Coalway Junior in the UK approached this task systematically. She said:
The amount of 1 blocks you can fit in it is 10.
The amount of 2 blocks you can fit in it is 9.
The amount of 3 blocks you can fit in it is 8.
The amount of 4 blocks you can fit in it is 7.
The amount of 5 blocks you can fit in it is 6.
The amount of 6 blocks you can fit in it is 5.
The amount of 7 blocks you can fit in it is 4.
The amount of 8 blocks you can fit in it is 3.
The amount of 9 blocks you can fit in it is 2.
The amount of 10 blocks you can fit in it is 1.
There are 55 rectangles.
Well done, Melissa! How did you work out that this makes 55 rectangles altogether? Is there a quick way of adding up all those numbers?
Marie and Sophia from Phorms München in Germany used a very similar method, and sent in this picture to demonstrate:
Thank you both for sending in that very clear picture.
Luca from Highgate Junior School in the UK thought about this in a different way. Have a look at Luca's explanation and see if you can follow his method:
Well done Luca! Luca found all of the rectangles that started with the first small rectangle, then all of the rectangles that started with the second, all the way up to the rectangles that start with the final small rectangle (which will just be one rectangle). I wonder if we can expand Luca's method to find a way of counting all the rectangles inside a counting stick of any size?
Sophia from Highgate had a think about the general pattern. She said:
At first I looked at the problem and thought there were 10 rectangles (all the different coloured small rectangles). I soon realised that there would be many rectangles inside the larger rectangle and the larger rectangle as well so there would be a lot more than 10. I started by focusing on the first rectangle there was only one. I then went on to the second rectangle. I realised that there would be one rectangle that was the first two squares and a rectangle which was just the second rectangle. I then came up with a theory, my theory is that whatever rectangle you are on the rectangles that fit inside the rectangles before and the rectangle you are on would add up to how may rectangles would fit inside the current one. For example, take the fourth rectangle you would start by adding how many rectangles fit inside the first rectangle. Only one. You would then take the take the second rectangle. 2 new rectangles fit inside the second rectangle. If you add them together and then add them on to 3 since that is how many new rectangles fit inside the third rectangle you get 6. 6 rectangles fit inside the third rectangle. You then add this in to 4 since in the fourth rectangle you get 4 new rectangles. If you add 6 and 4 you get 10. This means that 10 rectangles fit inside the fourth rectangle. This is the formula to solve a problem like this. This would work all the way up to the hundreds and thousands.
This is a really interesting way of thinking about it, Sophia. I agree that the pattern works, and I wonder if anybody can explain why it works. Why do we add four new rectangles when we move from the counting stick of length three to the counting stick of length four?
Lots of other children also noticed that there is a pattern when we look at the rectangles inside counting sticks of different lengths. Angel from Highgate said:
When investigating the sequence I noticed that the difference between the terms went up by one each time starting with +2 then plus 3 then plus 4 etc.
Well done, Angel - this is a different way of thinking about Sophia's pattern.
We received lots of solutions pointing out that starting at 1 and following the pattern +2 +3 +4 gives us the triangle numbers, so well done to everybody who spotted this. Dhruv from St. Anne's RC Primary School sent in this table of results:
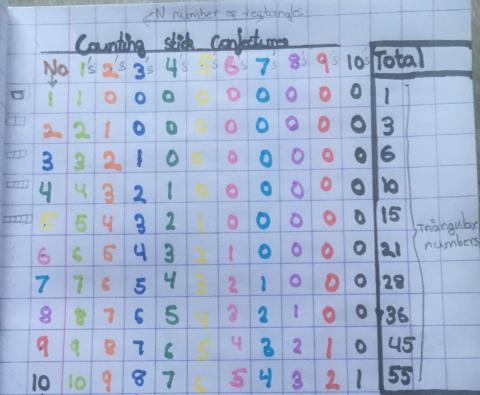
This table makes the pattern very clear - well done!
Some children thought about quicker ways of adding the numbers of rectangles inside a counting square. Anya from Highgate noticed that the numbers in the sum 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 can be put into pairs that make 11. Have a look at Anya's full solution. I wonder what each pair of numbers might add up to if we change the length of the counting stick?
Oscar from Highgate used the fact that the pairs of numbers make 11 to find a quick way of adding up the numbers. He explained:
If I look at the entire ten box rectangle, there can only be one ten box rectangle. But if I look at nine box rectangles there are two possibilities: 1-9 and 2-10. If I look at 8 box rectangles there are three possibilities, 1-8, 2-9, 3-10.
I have worked out that each time I decrease the number of boxes (that form each rectangle) by one, the number of possibilities increases by one. The total number of possibilities is the sum of the numbers 1-10 because it's 1+2+3+4+5+6+7+8+9+10. The sum is 55.
An easy way to figure out the sum of a sequence of consecutive numbers is to add the first and last numbers and multiply the result by the number of pairs of numbers. Here this would be 1 plus 10 = 11 x 5 (pairs) = 55
Well done, Oscar. How do you know that we can just add the first and last numbers and multiply the result by the number of pairs?
Aran from Highgate explained why this method works. He said:
There is a formula that can be used to quickly find the number of rectangles in large sticks.
Starting with the stick with 6 blocks, I noticed that you could add the numbers in a different order
1+6 = 7
2+5 = 7
3+4 = 7
I.e.: (half of six) multiplied by (6+1) = 21 rectangles
This also works for all the other numbers!
Aran went on to describe a way that we can use algebra to write this method:
The formula is: If x = the number of small rectangles on the stick then x divided by 2 multiplied by (x+1) equals the number of possible rectangles. This formula works with both odd and even numbers.
So, working out how many rectangles are in a stick with 100 rectangles is a lot faster and easier now. All you need to do is use the formula. 100 divided by 2 x (100+1) = 5050 and a stick with 1000 small rectangles would just be 500,500 rectangles.
Well done, Aran! From your example, I'm convinced that the formula works for 6, but I'm not yet convinced that it definitely works for bigger numbers. We received lots of solutions saying that the formula was x divided by 2 multiplied by (x+1), but not many children could explain why it would always work.
Dhruv drew a picture to show how to add the numbers in pairs when finding the number of rectangles inside the 100-length counting stick:
Thank you for sending this in, Dhruv, it makes it very clear that we are adding 101 together lots of times. It's slightly trickier to check that we should be adding it together 50 times. I wonder if anybody can explain why it needs to be added 50 times?
TaoHai thought about this formula in a different way. They sent in this explanation:
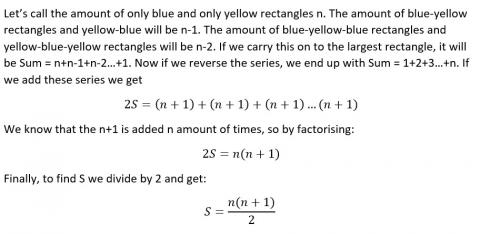
Well done for using algebra to prove that the formula always works! TaoHai has taken a counting stick of a general length of rectangles, n, and has called the sum of all of the rectangles inside it S. By reversing the list of numbers and adding the two lists together, we can show that two lots of S must be the same as adding n lots of n+1 together. This proves that the sum S is half of n multiplied by n+1.
Ci Hui Minh Ngoc from Kong Hwa School in Singapore explored what would happen if the 'counting stick' was a square rather than a long rectangle. Try this for yourself first - if you draw a square on a piece of squared paper, how many squares can you see inside your square altogether? Can you see a pattern in the answers if you begin with squares of different sizes? Have a look at Ci Hui Minh Ngoc's full solution to see what they found out.
Teachers' Resources
Counting Stick Conjectures
Have you ever seen a counting stick? You might have one in your classroom at school. Here is a photo of one:
What do you see?
What do you notice?
What would you like to ask?
Here is a simple picture of the counting stick:
How many rectangles can you see? (The rectangles may be different sizes.)
Once you've had a think about how many rectangles there might be, click below to see what Zoya thought.
Zoya says:
"I can see some small rectangles, which are either yellow or blue.
I can also see some bigger rectangles, made of two of the small ones. And some that are even bigger too.
I tried to count all the rectangles but I got very confused."
What might you suggest that would help Zoya?
Again, have a think and then click below to see what Max suggested.
Max says:
"Perhaps it would be easier if we started with a smaller counting stick.
We could try a counting stick with just two of the smallest rectangles, like this:
I think that has two small rectangles and one larger one, which makes three rectangles altogether.
Then we could try a counting stick with three smallest rectangles, like this:
This time I can see three very small rectangles, two blue and one yellow.
I can also see a rectangle which is made up of two of these small ones, which I've outlined in red:
And there's another one like this:
And then there is one large rectangle:
So, I think that makes six altogether.
If we do this a few more times with different sized sticks, perhaps we'll see a pattern."
Can you see how Max worked out the total number of rectangles each time?
Try out his suggestion. How many rectangles are there on a counting stick which is made up of four small squares? Five squares? Six...?
What do you notice? Can you see a pattern?
Is there a quick way to work out how many rectangles there would be, for a counting stick with 100 sections? Or 1000? Or...
How can you be sure that what you have noticed will always be true?
Mathematicians aren't usually satisfied with a few examples to convince themselves that something is always true.
Can you provide an argument that would convince mathematicians?
Why do this problem?
This task encourages learners to connect geometrical and numerical ideas, and not to be put-off if a problem seems unmanageable at first. In this case, simplifying the task, generating different examples and then looking for patterns will give children the opportunity to make conjectures and develop mathematical arguments to prove or disprove them.
Possible approach
This problem featured in an NRICH Primary webinar in March 2022.
If you have a counting stick, you could use it to introduce the task, but it is not essential. Whether using a real stick or the photograph, give the whole group time to talk in pairs about what they see and what they might like to ask. Gather everyone together to share some of their observations and their questions, encouraging learners themselves to respond to the ideas of others. Try to welcome all contributions, even those that seem less mathematical!
If it hasn't come up naturally, lead into the idea of the stick being made up of rectangles by showing the image of the whole stick in blue and yellow (as opposed to the photograph). Ask the group how many rectangles they can see, and give them time to talk in pairs. Draw out the idea that there are many differently sized rectangles represented in the image and then allow time for pairs to count the total number. They may like to keep track of their thinking on a whiteboard or on paper, and it might be helpful for pairs to have a print out of this sheet which contains several copies of the whole counting stick.
The intention here is that learners struggle to keep track. This is deliberate so don't leave them floundering for too long, instead draw everyone together and invite comments. Listen out for those who are trying to make sure they find all the rectangles, but who are perhaps struggling to work systematically. Ask the class what we can do about this. There seem to be so many rectangles...
The idea of simplifying a task may not be one that is familiar with your learners - it will depend on their experiences. You may like to reveal Max's suggestion on screen and read it out loud. Give everyone time to take in Max's strategy and encourage pupils to ask questions if they are not sure what Max means. You may like to distribute the work amongst the class so that some pairs work on sticks that are four small rectangles long, while others work on five/six. You can encourage pairs to check with another pair that they agree on the total before recording on the board for all to see. It may be useful to agree a common language for referring to the different sticks (e.g. a stick which is 1 long, or 2 long, meaning that it contains one very small rectangle or two very small rectangles).
Once you have agreed totals for four, five and six length sticks, ask the class what they notice. It may be helpful to tabulate the results so that they are in order (it would be useful to include the total number of rectangles for the smallest possible counting stick which only contains one small rectangle). Learners might express the pattern in different ways. Some may say that the total goes up by 1, then 2, then 3, then 4 etc. Others may notice that this could be expressed as 1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5... Others may recognise the totals (1, 3, 6, 10...) as triangular numbers. Use the pattern to predict the total for the full length counting stick (of ten small rectangles). You may like to refer to Carl Gauss' method for adding consecutive numbers quickly, see our article Clever Carl.
Explain that mathematicians aren't usually satisfied with a few examples to convince themselves that something is always true. Challenge the class to try to come up with a mathematical argument that would convince mathematicians. This is certainly not straightforward, but as children discuss their thinking, listen out for learners who have an understanding of the fact that each stick contains the previous stick, plus one more little rectangle. This means the total number of rectangles will be the total of the previous stick, plus one more smallest rectangle, plus one more rectangle that is two long, plus... Help all learners get to grips with this, if appropriate, by sketching on the board.
Key questions
How many of the smallest rectangles are there in this stick?
How many rectangles are there which are 'two long'?
How are you keeping track of the total you've got so far?
Can you explain the pattern you can see to someone else?
Possible support
Encourage learners to use any manipulative that they find helpful to access this task. Some may want to be able to physically 'break up' the stick into the different sized rectangles to help in the process of working systematically.
Possible extension
A few learners might like to consider what happens when you consider the total number of squares on a chessboard. Can they simplify that problem in a similar way?