Playing squash
Image

In the game of squash, players gain "points'' by winning
"rallies''. If the "server'' wins a rally, he or she wins a point;
otherwise the service changes hands with no points gained. In
theory the game could go on for ever with each player losing all
their serves. Note that if in two consecutive rallies both players
lose their serve, then the situation is exactly the same as it was
before these two serves.
Normally the game is won by the first player to reach 9
points, typically by 2 or more points. But if the score reaches 8-8
then the person due to receive serve can call "9'' (in which case
the first to reach 9 wins) or call "10'' (in which case the first
to reach 10 wins). In December 2000 the problem was set of deciding
whether a player should call "9'' or "10'' if that player has a
fixed probability of winning any particular rally, regardless of
whether serving or receiving.
We call the players A and B, and we assume that the
probability that A wins a rally is $p$, whether he serves or not,
and whatever the score is. The corresponding probability for B is
$q$, where $p+q=1$.
At any given time there are four outcomes to be considered,
namely A or B is the first to serve, and A or B wins the next
point. There may be many rallies before anyone scores this point We
are interested in finding the four probabilities:
\begin{equation*} Pr(\hbox{A wins the next point given that A
serves first})= \theta, \end{equation*} \begin{equation*}
Pr(\hbox{A wins the next point given that B serves first})=
\varphi, \end{equation*} \begin{equation*} Pr(\hbox{B wins the next
point given that A serves first})= \lambda, \end{equation*}
\begin{equation*} Pr(\hbox{B wins the next point given that B
serves first})= \mu. \end{equation*}
Let us find $\theta$. One possibility is that $A$ wins the
first rally, and hence the first point; he does this with
probability $p$. If not, he loses it with probability $q$ and $B$
then serves. Then for $A$ to win the next point he must win the
next rally (with probability $p$) and then the situation returns to
that in which $A$ serves and wins the next point with probability
$\theta$. Thus $\theta = p + qp\theta$, and hence \[Pr(\hbox{A wins
the next point given that A serves first})= \theta = {p\over
1-pq}.\] Next, we find $\varphi$. As $B$ serves first, $A$ must win
the next rally (with probability $p$). The position now is that $A$
is serving and must win the next point (which he does with
probability $\theta$). Thus $\varphi = p\theta$, and hence \[
Pr(\hbox{A wins the next point given that B serves first})= \varphi
={p^2\over 1-pq}.\] By interchanging $A$ with $B$, and $p$ with
$q$, we see that \[Pr(\hbox{B wins the next point given that A
serves first})= \lambda ={q^2\over 1-pq},\] and \[Pr(\hbox{B wins
the next point given that B serves first})= \mu ={q\over 1-pq}.\]
Note that \[ Pr(\hbox{A or B wins the next point given that B
serves first})= \varphi + \mu, \] and \[\varphi + \mu = {p^2\over
1-pq}+ {q\over 1-pq} ={p(1-q)+q\over 1-pq}={p+q-pq\over
1-pq}={1-pq\over 1-pq}=1.\] It follows that if $B$ serves first,
then the probability that $A$ or $B$ eventually wins a point is
one; hence the probability that
the game goes on for ever is zero! You may like to draw a
tree diagram to illustrate this, and you will find that a
succession of rallies in which nobody scores a point is represented
by a long 'zig-zag' in your tree diagram. The start of the tree
diagram is given below.
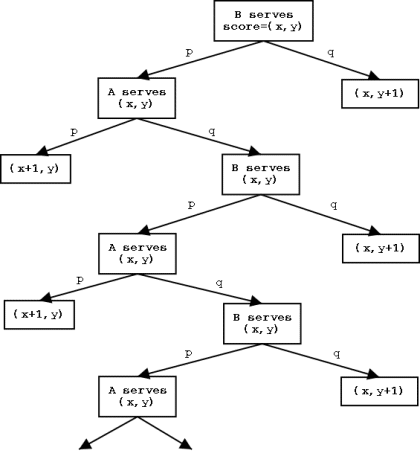
Image

The rules of squash say that if the position is reached when the score is $(8,8)$ (we give A's score first), and $B$ is to serve, then $A$ must choose between the game ending when the first player reaches $9$ or when the first player reaches $10$. We want to decide what is the best choice for $A$ to make (when $p$ and $q$ are known).
If $A$ chooses $9$, then he wins the game with probability $\varphi$. Suppose now that $A$ chooses $10$; then the sequence of possible scores and their associated probabilities are as follows:
| Sequence of scores | Probability | Probability in terms of $p,q$ |
|---|---|---|
| $(8,8) \to (9,8) \to (10,8)$ | $\varphi \times \theta$ | $p^3/(1-pq)^2$ |
| $(8,8)\to (8,9)\to (9,9) \to (10,9)$ | $\mu\times\varphi\times\theta$ | $p^3q/(1-pq)^3$ |
| $(8,8) \to (9,8) \to (9,9) \to (10,9)$ | $\varphi \times \lambda\times \varphi$ | $p^4q^2/(1-pq)^3$ |
It follows that the choice of $9$ by $A$ is best for $A$ if
$\varphi > \varphi\theta + \mu\varphi\theta + \varphi^2\lambda$,
or, equivalently, $1 > \theta + \mu\theta + \varphi\lambda$. In
terms of $p$ and $q$ this inequality is \[1 > {p\over 1-pq} +
{pq\over (1-pq)^2} + {p^2q^2\over (1-pq)^2},\] and this is
equivalent to \[(1-pq)^2 > p(1-pq)+pq+p^2q^2.\] After
simplification (remember that $p+q=1$), this is equivalent to
$p^2-3p+1> 0$. This means that $A$ should choose $9$ if $p <
0.38$ and should choose $10$ if $p> 0.38$.
[See the problem
Squash on the NRICH site.]
