Nested Squares
What proportion of the diagram is shaded?
Problem
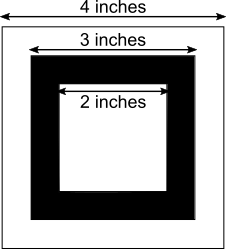
The diagram shows three nested squares.
What proportion of the diagram is shaded?
This problem is taken from the World Mathematics Championships
Student Solutions
Splitting the diagram into one-inch squares
The largest square is 4 squares long, and the smallest square in the middle is 2 squares long.
Then, we can put the shaded pieces together to make whole square inches.



So there are 5 shaded squares, out of 16 squares in total.
So the proportion of the area which is shaded is $\frac5{16}$.
Finding the areas of the squares
The whole diagram is a 4 inch by 4 inch square, so has area 4$\times$4 = 16 square inches.
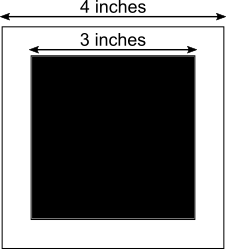
The shaded part is contained within a 3 by 3 square, so has area 3$\times$3 = 9 square inches.
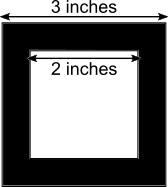
There is a hole in the shaded part, which is a 2 by 2 square. So the area of the hole is 2$\times$2 = 4 square inches.
So the area of the shaded part is
9$-$4 = 5 square inches.
So the proportion of the area which is shaded is $\frac5{16}$.
