Bundles of Cubes
Watch this animation. What do you notice? What happens when you try more or fewer cubes in a bundle?
Problem
In this challenge, we will be making 'bundles' of cubes.
We are going to start by making bundles of four cubes.
In the animation below, we start with one bundle and add an extra cube on its own, making five cubes altogether.
See what happens as we have more bundles and still keep just one extra cube:
We are going to start by making bundles of four cubes.
In the animation below, we start with one bundle and add an extra cube on its own, making five cubes altogether.
See what happens as we have more bundles and still keep just one extra cube:
What do you notice?
Can you explain your noticings?
We could then look at using a bundle of a different size. In the pictures below we see the same idea with bundles of six cubes and eight cubes:
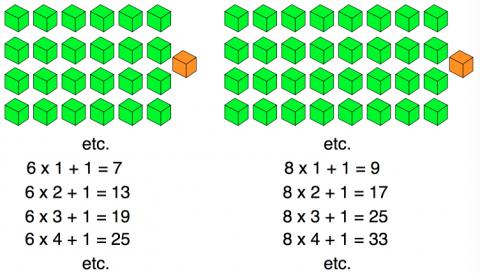
The images above stop at 'four lots' but you could try going much further, maybe up to sixteen lots.
What happens when the bundles are of five, seven or nine cubes?
When you've done some exploring and got some results, then compare your results for the different sizes of bundles.
What do you notice?
Can you explain any of your noticings?
Can you explain your noticings?
We could then look at using a bundle of a different size. In the pictures below we see the same idea with bundles of six cubes and eight cubes:
Image

The images above stop at 'four lots' but you could try going much further, maybe up to sixteen lots.
What happens when the bundles are of five, seven or nine cubes?
When you've done some exploring and got some results, then compare your results for the different sizes of bundles.
What do you notice?
Can you explain any of your noticings?
Getting Started
How will you keep track of what you're doing?
Might it help to have some 'things' to move around, such as cubes, or pebbles, or pasta shapes...?
Might it help to have some 'things' to move around, such as cubes, or pebbles, or pasta shapes...?
Student Solutions
Rahini from Emirates International School Meadows in Dubai wrote the following:
- I notice in the animation that you keep on adding four cubes but there is an extra cube on the side which is the same.
- When the bundles are of five, seven or nine cubes, the cubes multiply by that certain number plus one.
- I notice that the bundles are bigger and even the numbers are bigger.
- This happens because it depends on the number you're dealing with.
Thank you Rahini. If you have a go at this task, please do send us your ideas.
- I notice in the animation that you keep on adding four cubes but there is an extra cube on the side which is the same.
- When the bundles are of five, seven or nine cubes, the cubes multiply by that certain number plus one.
- I notice that the bundles are bigger and even the numbers are bigger.
- This happens because it depends on the number you're dealing with.
Thank you Rahini. If you have a go at this task, please do send us your ideas.
Teachers' Resources
Why do this problem?
This activity is designed to nurture children's curiosity by introducing novel mathematics - in this case the idea of multiplying then adding one as represented by 'bundles' of cubes. Children might end up pursuing different ideas from each other and this freedom to explore may well encourage learners to persevere more than they might usually. The task also offers opportunities for noticing patterns, conjecturing, explaining and generalising. (The further note at the foot of this page offers more support on curiosity in the classroom generally.)Possible approach
Rather than saying anything at all, you could show the short animation to the class and invite them to watch in silence at first. Alternatively, you could make the arrangements shown below using real cubes or other objects and laying them out on the floor/table:Image
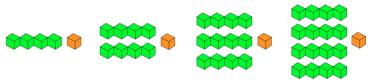
Once you have played the animation perhaps twice, ask learners to talk to each other about what they saw. Bring everyone together to develop a shared vocabulary for what is going on (you may introduce the term 'bundle' or children might have their own word/s). Take some time to share what they notice, trying to value all contributions, and encourage the group to unpick reasons for any patterns that they observe.
Once you feel that learners have got to grips with the context, introduce the idea that 'bundles' can have more/fewer cubes and invite them to explore. Pause at various points to faciliate mini plenaries so that ideas, thoughts and comments can be voiced. Emphasise that you are looking for reasons that a pattern occurs, not simply an observation that there is a pattern.
It might be appropriate for pairs/groups to create a poster of their findings, which could be presented to the rest of the group during the plenary. (This task may well benefit from having more than one lesson devoted to it.)
Key questions
Tell me about what you're doing.What ideas are you trying out?
What have you found so far? How would you explain any of your findings?
Possible extension
Some other ideas may come from looking at totals that are square numbers, prime numbers, multiples of 3 and multiples of 5, for example.Possible support
Some pupils may need manipulatives such as cubes or counters to set up each situation so that they can count rather than have to multiply.Further note
You may be interested in the following talks given by Professor Susan Engels, which focus on encouraging curiosity and are available on YouTube:The Rise and Fall of Curiosity - the extract from 23.50 to 37.15 on adult encouragement and teacher behaviour is particularly worth viewing
The Hungry Mind: The Origins of Curiosity - the extract from 8.22 to 12.29 on children asking questions is especially useful.
