Square Within a Square Within...
What fraction of this square is shaded?
Problem

The diagram shows a square within a square within a square within a square. Find the fraction of the area that is shaded.
This problem is taken from the World Mathematics Championships
Student Solutions
Splitting the diagram up into congruent shapes
Drawing lines through the corners of the smallest square, and then extending these, lots of the triangles are split in half to create lots of triangles the same size. Then extending the sides of the smaller white square, a pattern of squares becomes visible.

The diagram is made up of 4 little squares by 4 little squares, so 16 little squares altogether.
Count the number of squares which are half-shaded. There are 12 little shares which are half-shaded, so the same as 6 shaded squares.
So 6 out of 16 squares are shaded, which is $\frac6{16}=\frac38$ of the diagram.
Finding the relationship between the areas of the squares
Consider one square within a square, tilted in this way. By drawing on the diagonals of the shaded square, 4 smaller squares can be formed (each shown in a different colour on the right). Half of each of these squares is shaded, so the shaded square occupies half of the whole square.
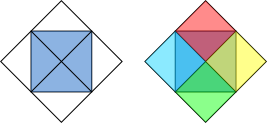
Now consider the squares below. The first square is the outline of the diagram. The area of the first blue square is half of the area of the diagram. The area of the next white square is half of the area of the first blue square, so $\frac14$ of the area of the diagram. The area of the second blue square is half of the area of the second white square, so $\frac18$ of the area of the diagram.

So the shaded area is $\frac12-\frac14+\frac18=\frac48-\frac28+\frac18=\frac38$ of the area of the diagram.
Rearranging the shaded triangles
Consider this part of the diagram. Because the lines marked are parallel, the shaded triangle on the outside is congruent to half of the smallest square (which is shaded).

Now consider moving the triangles around, so that they are 'back to back' and form new, larger triangles. Removing some of the lines makes it clear that 3 out of 8 triangles in the diagram are shaded:


So the fraction of the diagram that is shaded is $\frac38$.
